Algebraic and trigonometric skills
Dividing and factorising polynomial expressions
A polynomial is an algebraic expression involving many terms and can be factorised using long division or synthetic division.
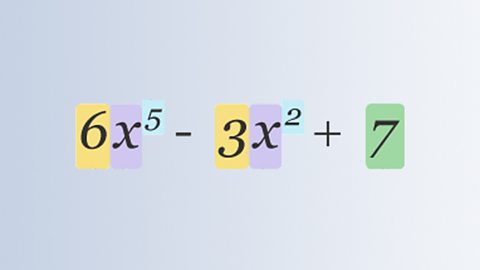
Laws of logarithms and exponents
Revise what logarithms are and how to use the 'log' buttons on a scientific calculator

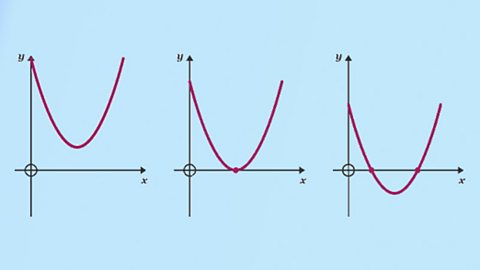
Solving polynomial equations
The nature and co-ordinates of roots can be determined using the discriminant and solving polynomials.
Solving logarithmic and exponential equations
Revise the laws of logarithms in order to solve logarithmic and exponential equations

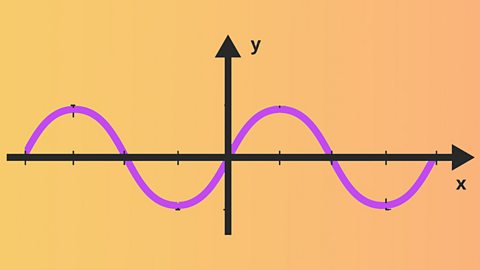
Trigonometric expressions
The addition formulae and trigonometric identities are used to simplify or evaluate trigonometric expressions. Trigonometric equations are solved using a double angle formulae and the wave function.

Solving trigonometric equations
Trigonometric equations can be solved in degrees or radians using CAST and its period to find other solutions within the range, including multiple or compound angles and the wave function.
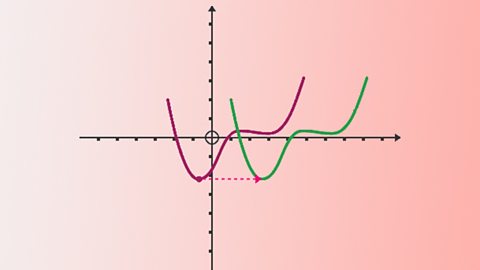
Identifying and sketching related functions
The rules from graph translations are used to sketch the derived, inverse or other related functions. Complete the square to find turning points and find expression for composite functions.
Determining composite and inverse functions
Composite and inverse functions can be determined for trigonometric, logarithmic, exponential or algebraic functions.

Geometric skills
Geometric vectors
Vectors describe movement with both direction and magnitude. They can be added or subtracted to produce resultant vectors. The scalar product can be used to find the angle between vectors.
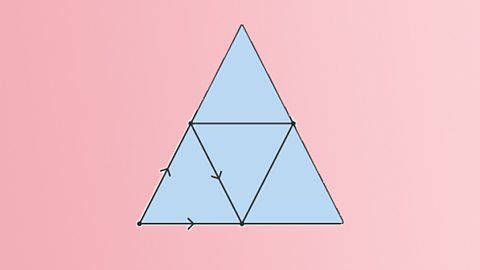
Working with vectors
Evaluate scalar product and determine the angle between two vectors

Calculus skills
Differentiation
Differentiation of algebraic and trigonometric expressions can be used for calculating rates of change, stationary points and their nature, or the gradient and equation of a tangent to a curve.

Integration
Integration is the inverse of differentiation of algebraic and trigonometric expressions involving brackets and powers. This can solve differential equations and evaluate definite integrals.
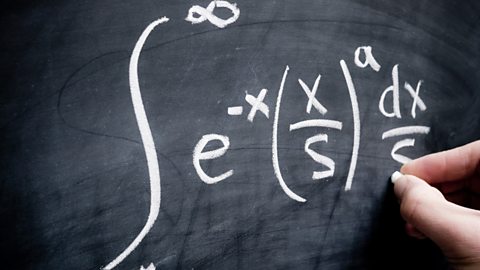
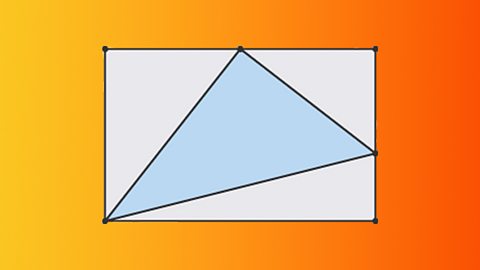
Applying differential calculus
Optimisation is used to find the greatest/least value(s) a function can take. This can involve creating the expression first. Also find the rate of change by differentiating then substituting.
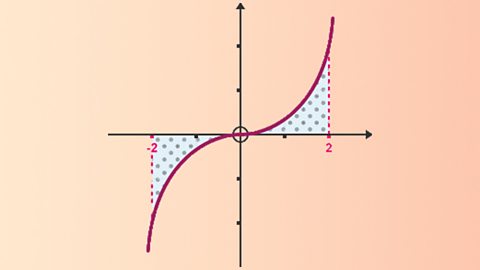
Applying integral calculus
The area above and below the x axis and the area between two curves is found by integrating, then evaluating from the limits of integration. Integration is also used to solve differential equations.
Algebraic and geometric skills
Rectilinear shapes
Find the gradient, equations and intersections of medians, altitudes and perpendicular bisectors using our knowledge of the mid-point as well as parallel and perpendicular lines.
Circles and graphs
The equation of a circle can be found using the centre and radius. The discriminant can determine the nature of intersections between two circles or a circle and a line to prove for tangency.
Sequences
A recurrence relation is a sequence that gives you a connection between two consecutive terms. This connection can be used to find next/previous terms, missing coefficients and its limit.

Links
- External linkExternal link
- External linkExternal link
- External linkExternal link
- External linkExternal link