Key points about standard form

standard formA number between 1 and 10 multiplied by a power of ten, eg 193 in standard form is written as 1·93 × 10², 0·193 in standard form is written as 1·93 ×10⁻¹. It is used as notation for very large and very small numbers. It is also called standard index form or scientific notation. is a way of writing very large and very small numbers so that they are easier to understand and work with.
Any number in standard form is written as: 𝐴 × 10\(^𝑛\).
The powerHow many times to use the number in a multiplication. For example, 3² is 3 to the power 2 or 3 x 3 or 3 squared. of ten is positive for numbers greater than 10 and negative for values less than 1.
Refresh your knowledge with these guides on place value as well as multiplying and dividing by powers of ten.
Video – Converting between ordinary numbers and standard form
Watch this video to find out what standard form is and learn how to convert between standard form and ordinary numbers, using some example questions.
Converting between ordinary numbers and standard form.
The number 10 is central to the place value system, and it can be raised to many different powers. When 10 is raised to positive integer powers, it gets 10 times bigger each time the power increases. So, the 1 digit will move left to the 10s column, then to the 100s, then to the 1000s, and so on.
Remember, integer just means a whole number, positive or negative.
But when 10 is raised to negative integer powers, it gets 10 times smaller each time the power decreases. So, the 1 digit will move right to the 10ths column, then to the 100ths, then to the 1000ths, and so on.
You can use this knowledge to express numbers in standard form, which is often used when representing very big or very small numbers.
A number written in standard form always has the form: 𝐴 multiplied by 10 to the power of 𝑛, where 𝐴 is a number greater than or equal to 1, but less than 10, and 𝑛 is any integer.
For example, to write 3200 in standard form. Place the digits in the place value table so that they form a number between 1 and 10. 3.2 is between 1 and 10, so this is your 𝐴 value.
Then, to find 𝑛, move the digits left until you get 3200. Moving one place left is equivalent to multiplying by 10 to the power of 1. Two places left is equivalent to multiplying by 10 to the 2, and three places left is equivalent to multiplying by 10 to the 3.
The number in the place value table is now 3200. So, 3200 is written in standard form as 3.2 times 10 to the power of 3.
Let's look at some more examples.
Question 1: Write the ordinary number 136,000 in standard form.
Remember, when expressing the value in standard form, the first number, so your 𝐴 value, needs to be between 1 and 10.
So, for 136,000, the first number will be 1.36. It can't be 0.136 or 13.6 or 136, because these numbers are not between 1 and 10.
Starting with 1.36 in the place value table, move the digits left until you get to 136,000. To do this, you have to multiply by 10 to the power of 5. So, written in standard form, 136,000 is equal to 1.36 times 10 to the power of 5.
OK. Another question: Write 2.3 times 10 to the – 6 as an ordinary number.
The power is – 6. So this means 2.3 is being divided by 10 six times. Finally, count the place value columns to work out the answer. So, 2.3 times 10 to the – 6, written as an ordinary number, is 0.0000023.
Check your understanding
How to write a number in standard form
A number in standard form is written as 𝐴 × 10\(^𝑛\), where 𝐴 is a number that is greater or equal to one and less than 10 (1 ≤ 𝐴 <10) and 𝑛 is an integer.
𝐴 can be written as a decimal but not as a fraction.
Follow the working out below
GCSE exam-style questions
- Which number is written in standard form?
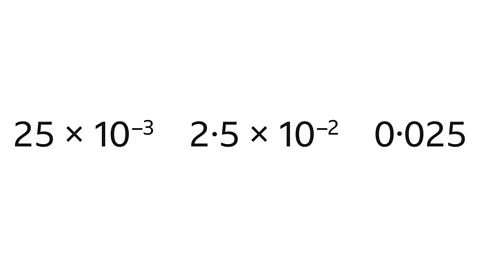
2·5 × 10\(^−\)\(^2\) is written in standard form.

25 × 10\(^−\)\(^3\) is a number greater than ten, multiplied by an integer power of ten. This is not in standard form.
2·5 × 10\(^−\)\(^2\) is a number greater than one and less than ten, multiplied by an integer power of ten. This is in standard form.
0·025 is a number less than one and it has not been multiplied by a power of ten. This is not in standard form.
- Which number is written in standard form?
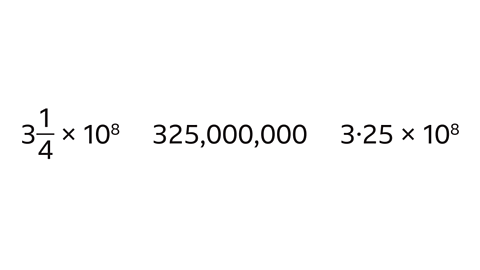
3·25 × 10\(^8\) is written in standard form.

3¼ × 10\(^8\) is a mixed number greater than one and less than ten, multiplied by an integer power of ten. This is not in standard form however because the number is not written as a decimal. It is a mixed number.
325,000,000 has been written just as a decimal number, which is greater than 10. This has not been written in standard form.
3·25 × 10\(^8\) is a number between one and ten multiplied by an integer power of ten. This is in standard form.
Video - Standard form hack
Watch this video to learn some simple hacks to help understand positive and negative power patterns in standard form.
Here's a handy hack to help you handle all the zeros in standard form conversions.
Let's look at the positive and negative power patterns that you may come across in your exams.
First up, the positive. For 10 to the power of 6, this is 10 multiplied by itself six times.
So, 10 times 10 times 10 times 10 times 10 times 10. There are six zeros after the 1 which, is 1 million.
10 to the power of 5 is five zeros after the 1, which is 100,000.
10 to the power of 4 has four zeros after the 1, which equals 10,000. 10 to the power of 3 has three zeros, which is 1000.
10 to the power of 2 has two zeros, which is 100.
10 to the power of 1 has one zero, which is 10, and 10 to the power of 0 is no zeros, so just one.
But, when working with standard form numbers that have a negative power of 10, it's not quite as simple.
10 to the power of negative 6 is 1 divided by 10 multiplied by itself six times. So, 10 times. 10 times. 10 times. 10 times. 10 times 10, which is one divided by a million, which equals 0.000001.
Notice how there are only five zeros after the decimal point. This is one less than the value of the power.
And this is the same for all negative powers of 10.
10 to the power of negative 6 has five zeros after the decimal point, which equals 0.000001.
10 to the power of negative 5 has four zeros after the decimal point, which is 0.00001.
10 to the power of negative 4 has three zeros after the decimal point.
10 to the power of negative 3 has two zeros.
10 to the power of negative 2 has one zero, so it's 0.01.
10 to the power of negative 1 has no zeros after the decimal point, so it's just 0.1.
Putting in an extra zero for negative power conversions is a common mistake, so try and remember that negative powers mean one fewer zero than the power after the decimal point.
How to convert numbers ≥1 to standard form
To write a number, greater or equal to one, in standard form:
Write the number as a value between 1 and 10.
The first non-zero digit is in the units column, followed by the decimal point and the remaining digits.
Zeros at the end of the number are not needed.
For a single digit value, the decimal point is not needed.
Write × 10.
Write in the power of tenThe power of ten tells us how many times to use the number in a multiplication. For example 10² means 10 × 10 = 100. Powers of ten are 10, 100, 1000 and so on. .
For a number greater than or equal to 10, the power is a positive integer.
The power is found by counting the number of places the first non-zero digit has moved to the right. This is the number of times the value must be multiplied by 10 to get the original number.
For a number greater or equal to 1 and less than 10, the power is zero.
Follow the working out below
GCSE exam-style questions
- Write 300,000,000,000 in standard form.
3 × 10\(^1\)\(^1\)
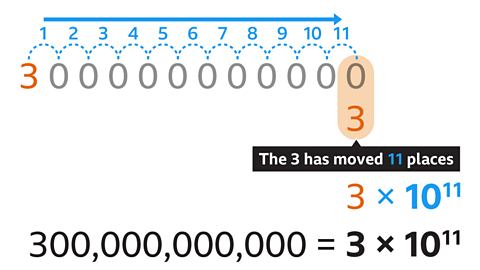
Write 300,000,000,000 as a value between 1 and 10. This is 3.
Write × 10 and the power of ten.
The power can be found by counting the number of places the first non-zero digit (3) has moved to the right.
The digit 3 has moved 11 places. The power of ten is eleven.
- Write 296,000 in standard form.
2·96 × 10\(^5\)
Write 296,000 as a value between 1 and 10. This is 2·96.
Write × 10 and the power of ten.
The power can be found by counting the number of places the first non-zero digit (2) has moved to the right.
The digit 2 has moved 5 places. The power of ten is five.
How to use standard form to express small numbers
To write a number less than 1 in standard form:
Write the number as a value between 1 and 10.
The first non-zero digit is in the units column, followed by the decimal point and the remaining digits.
The zeros in front of the units digit are not needed.
For a single digit value, the decimal point is not needed.
Write × 10.
Write in the power of tenThe power of ten tells us how many times to use the number in a multiplication. For example 10² means 10 × 10 = 100. Powers of ten are 10, 100, 1000 and so on. .
For a number less than 1, the power is a negative integer.
The power can be found by counting the number of places the first non-zero digit has moved to the left.
This is the number of times the value must be multiplied by \(\frac{1}{10}\) (or divided by 10) to get the original number.
Follow the working out below
GCSE exam-style questions
- Write 0·08754 in standard form.
8·754 × 10\(^–\)\(^2\)
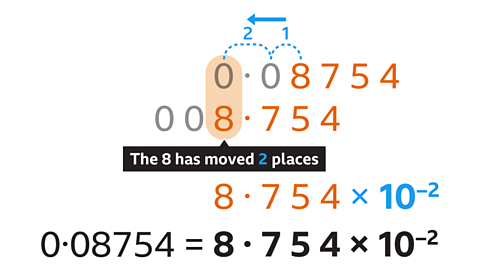
- Start by writing 0·08754 as a value between 1 and 10. This is 8·754.
- The first non-zero digit (8) is in the units column, followed by the decimal point and the rest of the digits (7, 5 and 4).
- The zeros in front of the 8 are not needed.
- Next write × 10 and the power of ten.
- 0·08754 is less than 1, the power is a negative integer.
- The power is found by counting the number of places the first non-zero digit (8) has moved to the left.
- The digit 8 has moved two places to the left, so the power of ten is –2.
- Write 0·000,000,06 in standard form.
6 × 10\(^–\)\(^8\)
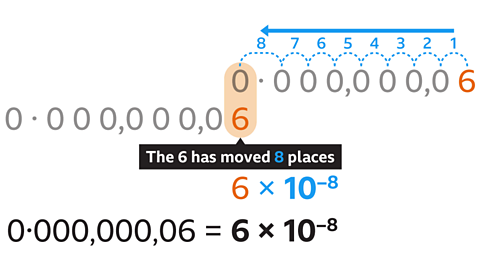
Start by writing 0·000,000,06 as a value between 1 and 10. This is 6.
The first non-zero digit (6) is in the units column.
There is only a single digit so the decimal point is not needed.
The zeros in front of the 6 are not needed.
Next write × 10 and the power of ten.
0·000,000,06 is less than 1, so the power is a negative integer.
The power is found by counting the number of places the first non-zero digit (6) has moved to the left.
The digit 6 has moved eight places to the left, so the power of ten is –8.
How to convert from standard form
To convert a standard form number 𝐴 × 10\(^𝑛\) to an ordinary (decimal) number, multiply the value 𝐴 by the power of ten:
Where 𝑛 is positive, the number is larger than 𝐴.
Each digit in 𝐴 moves 𝑛 places to the left.
Gaps between the digits of 𝐴 and the decimal point are filled with .
Where 𝑛 is negative, the number is smaller than 𝐴.
Each digit in 𝐴 moves 𝑛 places to the right.
Gaps between the digits of 𝐴 and the decimal point are filled with place holder zeros.
Where 𝑛 is zero, the ordinary number is the value of 𝐴.
It is important to have a good understanding of positive and negative powers of ten.
Follow the working out below
GCSE exam-style questions
- Write 2·5 × 10\(^6\) as an ordinary number.
2,500,000
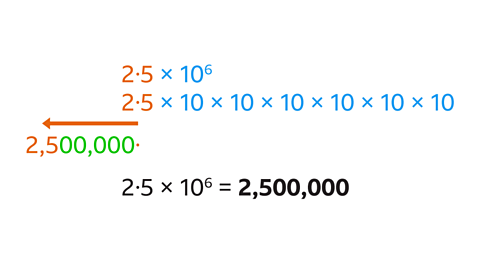
Multiply 2·5 by the power of ten (10\(^6\)).
- This is 2·5 × 10 × 10 × 10 × 10 × 10 × 10.
Each digit moves six places to the left.
Gaps between the digits 25 and the decimal point are filled with place holder zeros.
- Write 4·09 × 10\(^–\)\(^5\) as an ordinary number.
0·0000409
Multiply 4·09 by the power of ten (10\(^–\)\(^5\)).
10\(^–\)\(^5\) means \(\frac{1}{10}\) × \(\frac{1}{10}\) × \(\frac{1}{10}\) × \(\frac{1}{10}\) × \(\frac{1}{10}\), which is the same as dividing by ten five times, or multiplying by 0·00001.
To multiply 4·09 by 0∙00001 move the digits four places to the right.
Fill the gap behind the decimal point with place holder zeros so that the number has the correct value.
How to order numbers in standard form
For equal values of 𝐴 (in 𝐴 × 10\(^𝑛\)), the greater the power of ten (𝑛), the greater the value.
To compare and order numbers in standard form:
Start with the power of ten.
- The greater the power of ten, the greater the order of magnitude of the number.
If numbers have the same power of ten, consider the value of 𝐴 to compare them.
- Use understanding of ordering decimals for this process.
Review comparing and ordering decimals to support understanding of ordering numbers in standard form.
Follow the working out below
GCSE exam-style questions
- Write these numbers in order of size.
Start with the smallest number.

Smallest to greatest:
3·12 × 10⁻⁵, 2·31 × 10⁻⁴, 3·21 × 10⁻², 1·32 × 10⁰.

The numbers have different powers of ten.
The numbers can be ordered by placing the powers of ten in order from smallest to greatest.
The smallest power of ten is 10⁻⁵, the greatest is 10⁰.
10⁻⁴ is the second smallest and 10⁻² is the second greatest.
- Write these numbers in order of size.
Start with the greatest number.
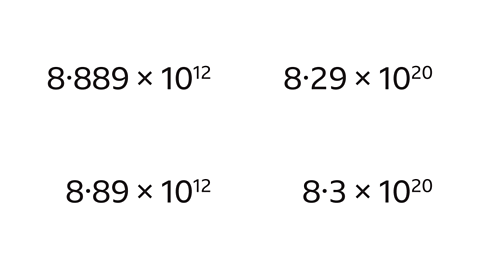
Greatest to smallest:
8·3 × 10²⁰, 8·29 × 10²⁰, 8·89 × 10¹², 8·889 × 10¹².

There are two different powers of ten, 10²⁰ is greater than 10¹².
Compare 8·29 × 10²⁰ and 8·3 × 10²⁰.
8·29 is less than 8·3, which means that 8·3 × 10²⁰ is greater than 8·29 × 10²⁰.
Compare 8·889 × 10¹² and 8·89 × 10¹².
8·889 is less than 8·89, so 8·89 × 10¹² is greater than 8·889 × 10¹².
Quiz – Standard form
Practise what you've learned about standard form with this quiz. The questions change each time you try, so keep testing your knowledge.
Now you have revised standard form, why not try fractions, decimals and percentages?
More on Number
Find out more by working through a topic
- count15 of 15

- count1 of 15

- count2 of 15

- count3 of 15
