Practising questions will help you to prepare for your maths exam. By working through example problems, you can build your confidence and sharpen your understanding of key topics including algebra, geometry and more.
These worked examples not only show you how to approach problems step-by-step but also include tailored tips for each topic to help you develop the skills to tackle similar questions on your own.
Use these questions to identify areas you feel confident in and those that need more practice.
Remember, the questions on the exam paper are not released until the day of the exam. The examples on this page are a guide to the topics and question structures that could be on the paper.
Top tips: probability and statistics
Use these targeted tips on using past papers to boost accuracy, tackle common question types and build exam confidence.
1. Describing a probability
Probability is estimating or calculating how likely or 'probable' something is to happen. A probability is written as a fraction or decimal, but don’t round the answer. For example, if the answer is \({1 \over 9}\) then leave the answer as a fraction. Don’t round it to 0.1 because 0.1 is \({1 \over 10}\).
2. Probability
The chance of an event happening can be described in words. For example ‘certain’, ‘impossible’ or ‘likely’. The probability of a certain event is 1 and the probability of an impossible event is 0. The answer to a probability question cannot be less than 0 or greater than 1. The sum of all outcomes of an event is 1.
If the probability that it rains on a particular day is \({1 \over 7}\) then the probability that it will not rain on that day is \({6 \over 7}\).
3. Set notation
There are some symbols you need to know. For example, if there are two sets: A and B, \(A \cap B\) is the intersection of the sets which means all the elements in both sets A and B.
\(A \cup B\) means A union B and means all the elements in set A or in set B. If you want to describe the elements not in a set use an apostrophe symbol. \(A'\) means all the elements not in set A.
4. Statistical diagrams
You need to work with several types of statistical diagrams and understand the differences between them. You should be able to draw these yourself or you may be asked to interpret a chart or diagram.
5. Statistical calculations
There are three different types of average - the mean, median and mode. You need to be able to calculate these from data and understand the advantages and disadvantages of each.
6. Comparing data
You may be asked to compare two sets of data. Look at an average: the mean, median or mode and how spread out the data is. Give these statistics and interpret them in the context of the question.
Worked example question
Four numbers have a mean of 20.
A fifth number is added to the set and the mean is now 19.
What number was added to the set? (3 marks)
The four numbers have a mean of 20 so the total of the four numbers is 80.
Call the new number n. The total of the five numbers is 80 + n.
The mean of the five numbers is 19, so:
\({80 + n \over 5}\) = 19
80 + n = 19 × 5 = 95
n = 95 - 80 = 15
The number added to the set was 15.
The first method mark is awarded for the four numbers totalling 80.
The second method mark is awarded for setting up the equation \({80 + n \over 5}\) = 19.
The third mark is for the correct answer of 19.
Top tips: Geometry
1. Vocabulary
There is a lot of vocabulary that you need to know for geometry. Do you know how to classify angles and the names and properties of different types of triangles and quadrilaterals? Do you know the correct wording for angle properties? Sometimes you are asked to give a reason for your answer, so you must correctly give a reason, such as “angles at a point add to 360°”. Do you know the names of the various parts of a circle?
2. Question wording
Read the question carefully, noting any vocabulary used, and don’t muddle terms up. Make sure you know the difference between area and perimeter. Make sure you know when to calculate an answer and when you are expected to take measurements from a diagram. If a question asks you to calculate or work out the answer, then you cannot find the answer by measuring from the diagram. The question wording will be very clear. Also check that you know the meaning of symbols used, such as those used to indicate parallel lines and how angles are named with three letters.
3. Transformations
As well as drawing shapes after a transformation, you may be asked to describe a transformation. Make sure you can fully describe reflections, rotations, translations and enlargements.
4. Constructions
Make sure you have all the equipment you need for the exam, including a pair of compasses. If you are using a ruler and compass to draw something - for example, a perpendicular bisector of a line or bisecting an angle - make sure you clearly show the compass arcs in your construction.
5. Geometry and algebra
Questions may use algebra and geometry skills. If you are finding the length of a side of a right-angled triangle and you know two of the sides you can use Pythagoras to find the length of the third side. You need to be careful to identify the hypotenuse and sides carefully and be able to use the formula for Pythagoras’ theorem. If you are given the hypotenuse and one side length, to find the other, you must rearrange the Pythagoras formula.
Worked example question
The diagram shows two right-angled triangles.
Calculate the size of the angle marked x.
Give the answer to 1 decimal place. (4 marks)
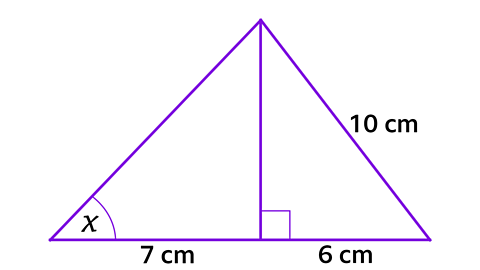
Both triangles have the same height (h).
Using Pythagoras’ theorem:
h2 + 62 = 102
Rearranging:
h2 = 102 - 62
h2 = 100 - 36 = 64
h = √64
h = 8 cm
Mark scheme:
To get the first mark for this question, show a correct method leading to the answer.
Rearranging the Pythagoras' formula to find the height, h2 = 102 - 62, would earn the method mark.
The answer mark is awarded for 8 cm.
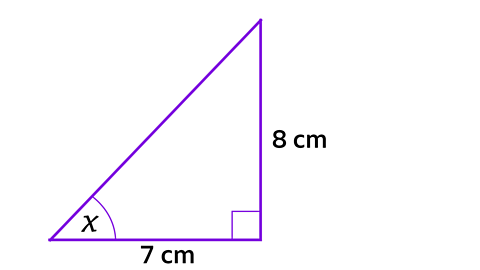
Now the height of the triangle is known, trigonometry can be used to find the angle marked x. In this triangle, identify the sides carefully.
The side of length 8 cm is opposite the angle x, and the side of length 7 cm is adjacent to the angle x. Use the tangent ratio:
tan x = \({8 \over 7}\)
x = tan-1 \({8 \over 7}\)
x = 48.8° (to one decimal place)
Method marks are given for correctly using the tangent ratio and applying the inverse function.
Remember to follow any instructions. The answer must be given to 1 decimal place.
Do not round until giving the final answer. When using the inverse tangent function, enter the exact value of \({8 \over 7}\).
Top tips: Ratio
1. Comparing quantities
Ratios are used to compare quantities. Equivalent ratios are formed by multiplying or dividing the numbers in the ratio by the same number. For example, the ratio 4 : 5 is equivalent to 12 : 15. The ratio 16 : 4 is equivalent to 4 : 1.
A ratio is usually written using integers, but you may be asked to write a ratio in the form 1 : n or n : 1, in this case n could be a decimal.
2. Simplest form
You may be asked to write a ratio in its simplest form. Work this out by looking for the highest common factor of the numbers in the ratio. 9 : 27 in its simplest form would be 1 : 3 as both numbers are divisible by 9.
3. Ratios and fractions
Understand the relationship between ratios and fractions. If red balls and green balls are in the ratio 3 : 5 then the fraction of red balls is \({3 \over 8}\) and the fraction of green balls is \({5 \over 8}\).
4. Units
The numbers in a ratio must be in the same units. To simplify the ratio 20 mm : 5 cm, first covert 5 cm to mm, 5 cm = 50 mm. The ratio is 20 : 50. The simplest form is 2 : 5.
Worked example question
The ratio of students in Group A to students in Group B is 5 : 6
There are 468 students in group B.
How many students are there altogether?
Group A : Group B
5 : 6
? : 468
To form an equivalent ratio we multiply both numbers in the ratio by the same number.
468 ÷ 6 = 78. Both numbers must be multiplied by 78.
The number of group A students is is 5 × 78 = 390.
Read the question carefully, we need the total number of students in the school, 390 + 468 = 858 students.
The first mark is for a valid method which leads to a correct answer, for example, working out the number of students in group B.
Or use an alternative method: \({6 \over 11}\) of the students are in group B, so we could work out \({1 \over 11}\) of the students which is 468 ÷ 6 = 78, giving a total number of students as 78 × 11 = 858.
Top tips: Number
1. Calculations
You should be able to do calculations with and without a calculator. Make sure you know how to add, subtract, multiply and divide positive and negative numbers including integers, decimals and fractions, and remember the correct order of operations.
2. Rounding
Make sure you can round numbers correctly. You should be able to round numbers to a given place value and to a given number of decimal places or significant figures. To help you think about limits of accuracy, this is like rounding but backwards. For example, if a length has been measured as 6 cm to the nearest cm, you need to decide the lowest value the actual length is. To do this, think about numbers that round up to 6 cm to the nearest cm. 5.9 cm rounds up to 6 cm, so does 5.8 cm. Which other numbers round up to 6 cm? How low can you go? 5.5 cm is the lowest value for the length.
3. Estimating
If you are asked for an estimate, you will not get any marks for an exact calculation. If you are asked to estimate a calculation then you should round the numbers in the calculation to numbers that are easier to work with; numbers can be rounded to 1 significant figure.
4. Fractions, decimals and percentages
You need to be able to convert between fractions, decimals, and percentages accurately. How would you change 5% to a fraction and to a decimal?
5% as a fraction is \({5 \over 100}\), which simplifies to \({1 \over 20}\)
As a decimal:
\({5 \over 100}\) = 0.05
Does the answer make sense? Is it a reasonable size?
If you thought 5% is 0.5; that can’t be correct because 0.5 is \({1 \over 2}\), which is 50%.
5. Reverse percentages
Sometimes a question on percentages is asking for the original amount before a percentage increase or decrease. Look carefully at the wording of the question to see if this is the case.
6. Indices
You may need to use indices. Make sure you know the laws of indices and remember that any number to the power zero is 1. For example, 7° = .1
7. Calculations involving time
Be careful when calculating time. You need to be able to convert between decimal form and hours and minutes. For example, 2.5 hours is 2 and a half hours which is 2 hours 30 minutes. 2.5 hours is not 2 hours 50 minutes.
Worked example question
1 (a) Write down the value of 60 (1)
(b) Write down the value of 3-2(1)
(a) 60 = 1, you need to know that any number raised to the power of 0 is 1.
(b) 3-2 = \({1 \over 3^2}\) = \({1 \over 9}\).
Top tips: Algebra
1. Calculations
Make sure you know how to add, subtract, multiply and divide with negative numbers. It is common to use negative numbers in algebra.
Remember the correct order of operations. For example, in the expression -3x2 only x is squared.
2. Vocabulary
It is important to know the meaning of the words you come across in algebra. For example, do you know the difference between an equation, a formula, an expression and an identity? Are you familiar with the command words in exam questions? For example, solve means to find the solution of an equation or inequality and factorise means you must insert brackets by taking out common factors.
3. Presentation
You may need several steps in your solution to a question on algebra. Keep your work organised by starting a new line for each step and write each line underneath the previous line. Doing this will help you achieve method marks even if your final answer is incorrect.
4. Check your work
When you solve an equation, substitute your answer back into the original equation to see if it works; if you factorise an expression, expand the brackets and see if you get back to the original.
If there are twice as many cakes as buns in a display. If c is the number of cakes and b is the number of buns, a question could ask you to write down the relationship between c and b. If you are not sure if the answer is c = 2b or b = 2c, try it out with some numbers.
Try c = 2b, if the number of buns is 5, then b = 5 and c = 2 × 5 = 10, with 10 cakes and 5 buns, there are twice as many cakes as buns.
5. Graphs
If you are asked to use a graph in a question, show your method by adding appropriate lines to the graph. For example, you could do this when using a conversion graph or solving an equation from a graph.
Worked example question
Factorise
a) 7x - x
b) 6ab3 - 3a2b
a) 7x - x2 + x(7 - x)
Check by expanding the brackets
x(7 - x) + 7x - x2
b) 6ab3 - 3a2b + 3ab(2b2 - a)
It may help to write the expression out fully, then identify the common factors.
6ab3 - 3a2b = 3 x 2 x a x b x b x b - 3 x a x a x b
6ab3 - 3a2b = 3ab(2b2 - a)
Revise maths
Explore more maths resources with the full range of help from Bitesize.
Podcasts - Study support
Study smarter and take care of your wellbeing with two Bitesize experts.

Exam-style questions for Edexcel maths
Try these quizzes based on GCSE maths past papers.

Maths - Edexcel
Pinpoint your areas to revise from the full list of GCSE maths topics.

Support - exams and revision
Exams can be stressful, but don't worry: we've got you. Check out our handy tips and advice for keeping on top of your studies and revision.

More on Exam practice
Find out more by working through a topic
- count1 of 4
- count2 of 4

- count3 of 4
