Maths Week Scotland 2021 - Problem 3 - Triangle areas

Problem 3 is all about equilateral triangles. (Will Problem 4 be about squares?)

Maths teacher Chris Smith is on your side and equal to solving this.

The Maths Week Scotland Daily Challenges have been set by the Scottish Mathematical Council.

Here's the problem:

Triangles ABC and XYZ are both equilateral.

In each case, what fraction of the triangle is shaded?

Have a look at the lengths that have been marked. Can they help you work out the area?Remember the triangles are equilateral.

Are there ways you can break the area of the triangles down into smaller parts?

Moving the triangles around might help too.

You might want to draw or cut out the triangles yourself to play around with.

Worked out the answer? Here's how you can do it.

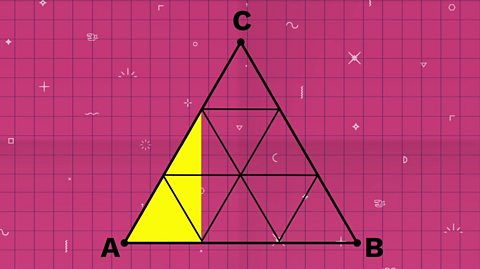
Triangle ABC

One way to work out what fraction of triangle ABC has been coloured in is to divide the area into nine smaller equilateral triangles.

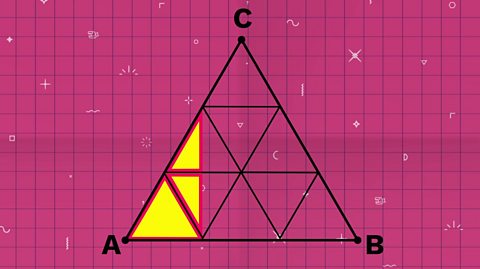
The coloured area is made up of 1 small triangles and two ½ triangles.

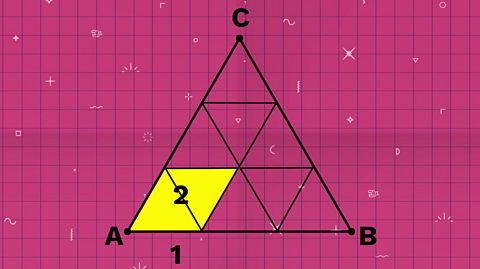
Moving the two half triangles together makes it easier to see that the total area covered is 2 small triangles.

The whole area is 9 small triangles.

So the coloured area is ²⁄₉ of the area of ABC.

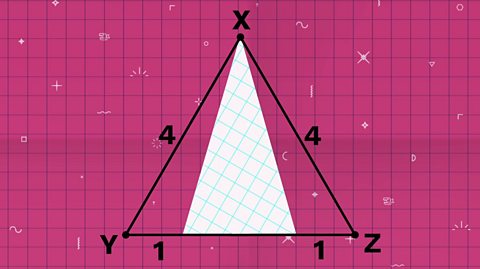
Triangle XYZ

Working out what fraction of triangle XYZ has been coloured is easier if you rotate the triangle so that side YZ becomes the base.

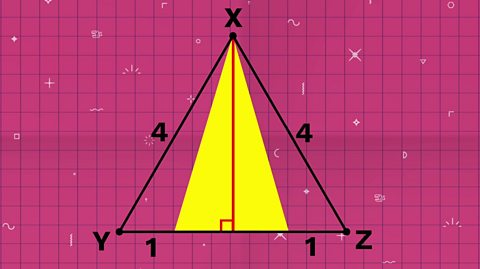
Now you can see that triangle XYZ and the coloured triangle both have the same height.

XYZ has sides 4 units long and there are two lengths of 1 unit on either side of the coloured triangle.

So the base of the coloured triangle is 2 units.

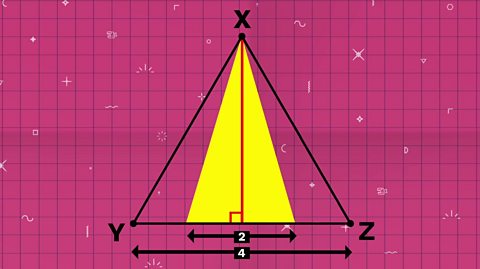
So the base of the coloured triangle is 2 units and the base of XYZ is 4 units. They both have the same height.

(2 X height) ÷ (4 X height) = ½

That means that the coloured triangle is ½ the area of XYZ.