Problem 7 - Number puzzle
Problem 7 is all about working out missing numbers.
Maths teacher Chris Smith has all the answers in mind.
The Maths Week Scotland Daily Challenges have been set by the Scottish Mathematical Council.
Chris Smith: In this problem you’re going to have to use maths to read my mind.
I’m thinking of three integers.
When I multiply the first two numbers together – let’s call them a and b - I get -6.
When I multiply the first and third – let’s call them a and c - I get -8.
The question is: can you work out what numbers I get when I multiply the second and third numbers in my brain together?
The key to unlocking this problem is working out all the possible integers that can multiply to give me the answers I was thinking of earlier.
Are there any numbers in common?
It's over to you to find out.

Chris is thinking of three whole numbers.
When the first two numbers are multiplied together, he gets -6.
ab = -6
When the first and third numbers are multiplied together, he gets -8.
ac = -8
Can you work out what numbers we get when the second and third numbers are multiplied together?
bc = ?

Need a hint?
The key to unlocking this problem is working out all the possible integers that can multiply to give me the answers I was thinking of earlier.
What combinations of a and b could multiply to make -6?And what combinations of a and c could multiply to make -8?
Are there any numbers in common?
Solution
Chris Smith: Did you manage to get the answers to our number puzzle?
Let’s take a look inside my brain.
Let’s call the three numbers in my head a , b and c.
We know that a times b is -6.
What integers would you need to multiply together to make -6?
It could be 1 times -6, -1 times 6, 6 times – 1 or -6 times 1.
Or 2 times -3, -2 times 3, 3 times -2 or -3 times 2.
But when we look at the next calculation, a times c = -8, we see that a has to be a factor of -8.
So a can’t possibly be -6, 6, 3 or -3 because none of those numbers can be multiplied by a whole number to make -8.
So that leaves us with four possibilities for a times b = -6 and four possible values of a.
So the possible answers are a, b, c equals
1, -6 and c,-1, 6 and c,2, -3 and cor -2, 3 and c.
We can then put those values into a times c equals -8. So a times c could be:
1 times -8, or -1 times 8, or 2 multiplied by -4, or -2 times 4.
We can now combine these possibilities together.
The question we wanted to answer was what do we get when we multiply the second and third of my secret numbers together (b and c)?
We now have enough information to work out the answer.
From the first two solutions, we get b times c equals 48, because both -6 times -8, and 6 times 8 equal 48.
And from the second pair of solutions, we have b times c equals 12, because -3 times -4 equals 12, and 3 times 4 equals 12.
So there are four sets of numbers but only two solutions: 48 and 12.
Let’s call the three unknown numbers a , b and c.
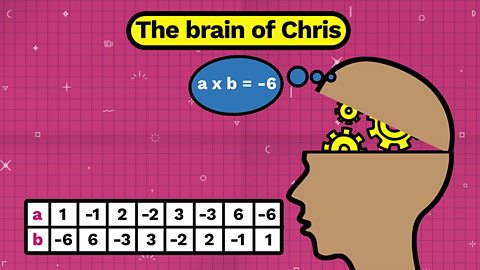
ab = -6
So a and b could be the following pairs of numbers:
1 x -6, -1 x 6
2 x -3 , -2 x 3
3 x -2, -3 x 2
6 x -1 , -6 x 1

ac = -8
This means a has to be a factor of -8.
So a can’t possibly be -6, 6, 3 or -3.
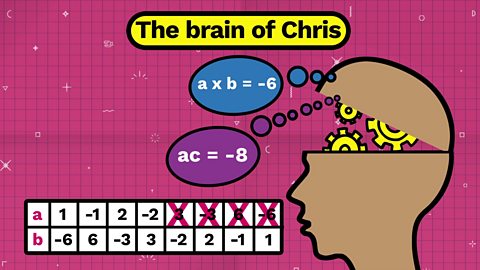
So that leaves us with four possibilities for ab = -6 and four possible pairs of values of a and b.
1 x -6, -1 x 6
2 x -3 , -2 x 3

We can then put those values into ac = -8. So ac could be:
1 x -8, -1 x 8
2 x -4, -2 x 4

We now have enough information to work out possible answers for bc = ?.
6 x 8 = 48
-6 x -8 = 48
3 x 4 = 12
-3 x -4 = 12
So there are four sets of numbers but only two solutions:
bc = 48 and bc =12.

More on Problem solving
Find out more by working through a topic
- count1 of 21

- count2 of 21

- count3 of 21

- count4 of 21
