Maths Week Scotland 2021 - Problem 6 - Filling the tank

Problem 6 is about working out the time it takes to fill a water tank.

Maths teacher Chris Smith has some top tips on how to solve this. Or should that be tap tips?

The Maths Week Scotland Daily Challenges have been set by the Scottish Mathematical Council.

There are three taps that can fill our water tank at different rates.

• The smallest tap takes 20 minutes to fill the tank.

• The medium tap takes 12 minutes to fill the tank.

• The biggest tap takes 5 minutes to fill the tank.

If we have all taps running at once, how long would they take to fill up the tank?

All of the taps run at different rates, so to be able to add them together you might need to find something that they all have in common.

You might look at how much of the tank each tap fills in a minute.

Or you could work out how many tanks each tap would fill in a longer period of time.

Worked out the answer? Here's how you can do it.

We know how long each tap takes to fill the tank.

To add them together we need to find out how much of the tank each tap fills in a certain time…for example one minute.

Run the taps for one minute

The small tap takes 20 minutes to fill the tank.

So in one minute it fills ¹⁄₂₀ of the tank.

The middle tap takes 12 minutes to fill the tank.

So it fills ¹⁄₁₂ of the tank in one minute.

The big tap takes 5 minutes to fill the tank.

So it fills ¹⁄₅ of the tank in one minute.

We can’t add ¹⁄₂₀ + ¹⁄₁₂ + ¹⁄₅ together as they are.

We can only add fractions if they have a common denominator, the number underneath,

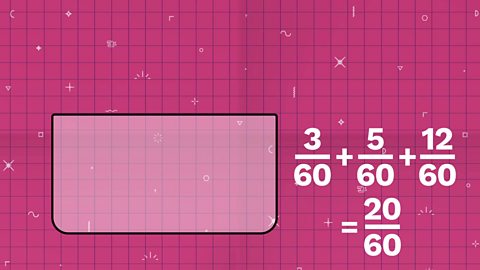
To do this we find a number that they all divide into – like 60.

¹⁄₂₀ + ¹⁄₁₂ + ¹⁄₅ = ³⁄₆₀ + ⁵⁄₆₀ + ¹²⁄₆₀

= ²⁰⁄₆₀

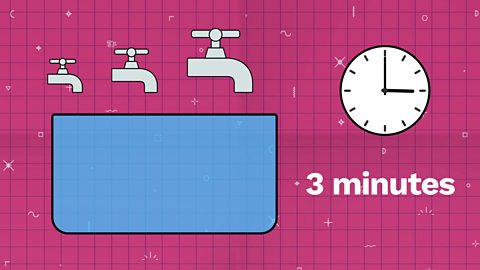
That cancels down to ¹⁄₃.

Which means with all three taps running we fill ¹⁄₃ of the tank in a minute.

So to fill the full tank takes 3 minutes.

Run the taps for one hour

Another way to solve this problem is to work out how many times each tap would fill the tank in one hour, sixty minutes.

The smallest tap takes 20 minutes to fill the tank.

So in an hour, it would fill the tank 3 times.

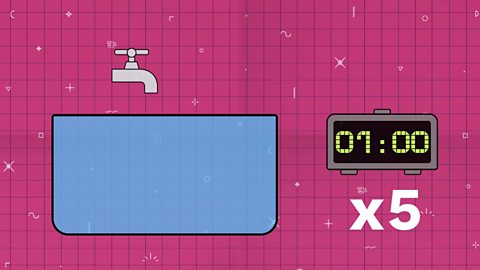
The middle tap fills the tank in 12 minutes.

It would fill the tank 5 times in an hour.

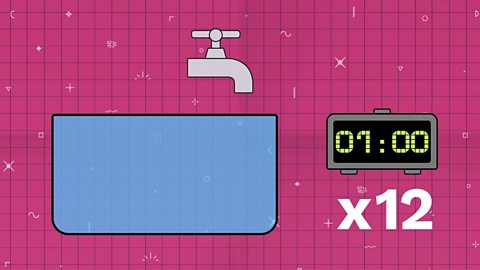
And the big tap fills it in 5 minutes.

So in a hour it would fill the tank 12 times over.

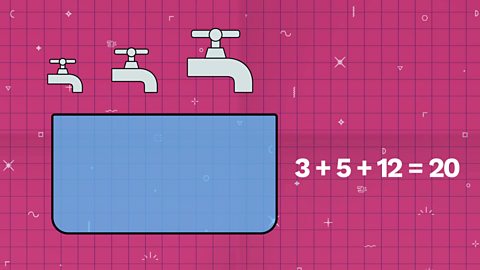
Add these together to work out how many times the three taps together would fill the tank in one hour:

3 + 5 + 12 = 20

Using all three taps we have filled our tank 20 times in an hour.

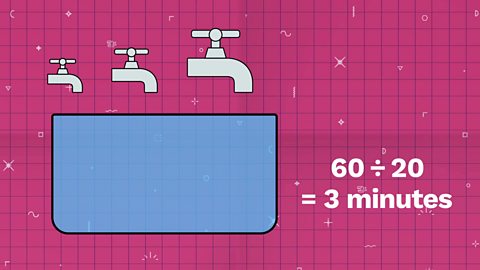
We want to know how long it takes to fill the tank one time. So we need to divide by 20.

60 ÷ 20 = 3

And that gives us the same final answer of 3 minutes.