How to do long multiplication using Napier's method – KS3 Maths

Key points

Napier’s method of multiplication is a method used to multiply large numbers when you do not have a calculator.
The advantage of Napier's method is that it only uses multiplication up to 9 x 9 and addition.
You can brush-up on times-tables with this game: Guardians: Defenders of Mathematica.

How to use Napier’s method of long multiplication

Multiplication using Napier's method uses a grid to multiply numbers.
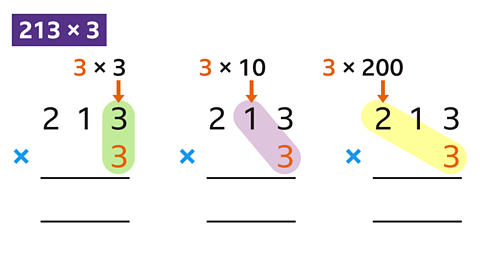
The grid layout depends on the calculation, eg 64 x 77 would need a 2 x 2 grid. For the calculation 321 x 36, either a 3 x 2 grid or a 2 x 3 grid could be used because multiplication is .
A diagonal line is drawn to separate the tens (T) and the units (U) in each box in the grid.
Each cell in the grid represents a two-digit answer to a multiplication made of a tens digit, and a units digit.

Example: calculate 37 x 91

Skip image gallery

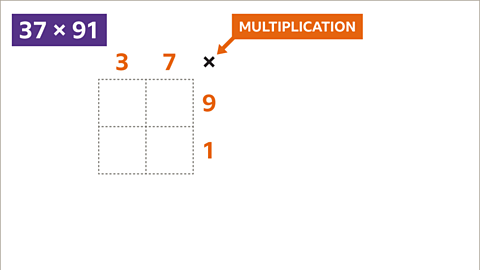
Image caption,
Draw a 2 by 2 grid to multiply a 2-digit number by another 2-digit number. Label the grid with figures at the top and the right-hand side.
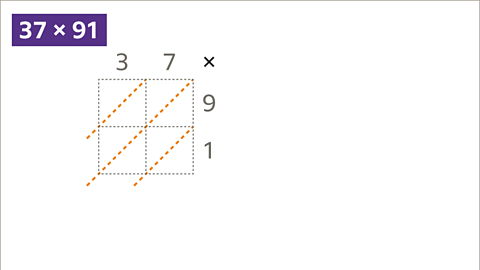
Image caption,
Draw the diagonals for each cell in the grid from top right to bottom left and extend outside the grid.
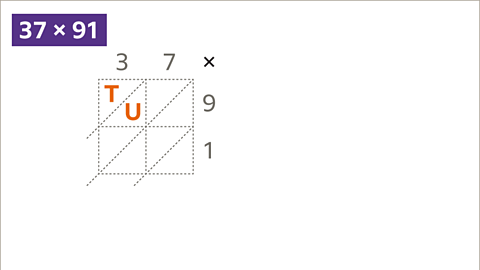
Image caption,
Each cell in the grid represents a two-digit answer to a multiplication (product) made of a tens digit, and a units digit.
Image caption,
This cell holds the product of 3 x 9. 3 x 9 is 27, 2 tens and 7 units.
Image caption,
This cell holds the product of 7 x 9. 7 x 9 is 63, 6 tens and 3 units.
Image caption,
This cell holds the product of 3 x 1. 3 x 1 is 3, 0 tens and 3 units.
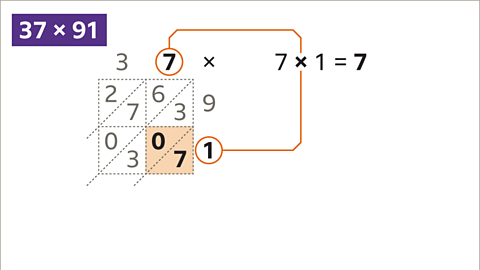
Image caption,
This cell holds the product of 7 x 1. 7 x 1 is 7, 0 tens and 7 units.
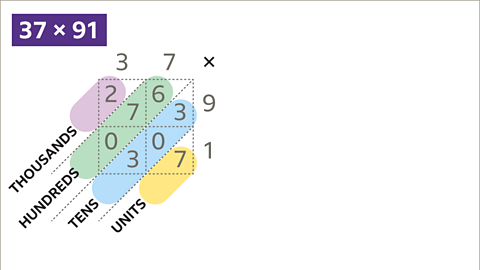
Image caption,
The grid is now filled with all the products. The sum of each diagonal gives part of the final answer. From right to left, the first diagonal is the units. The second diagonal is the tens. The third diagonal is the hundreds. The fourth diagonal is the thousands.
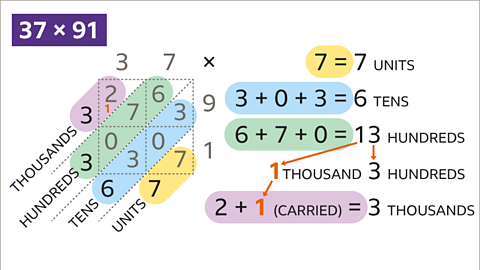
Image caption,
Add up each diagonal. Remember to carry when you get a two-digit answer.
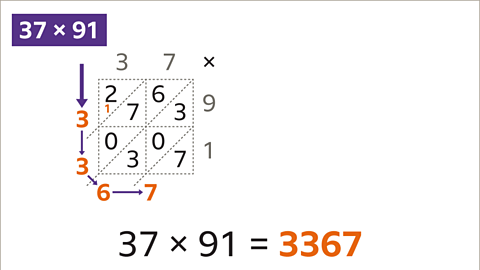
Image caption,
Follow the arrows to write the calculation with the answer: 37 x 91 = 3367

Example: calculate 653 x 72

Skip image gallery

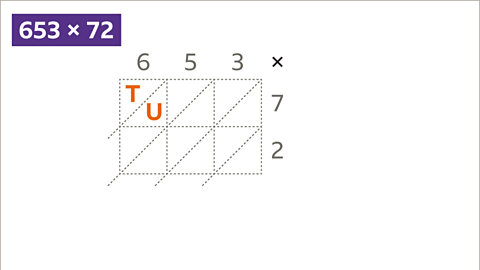
Image caption,
Draw and label the grid. Remember each cell in the grid represents a two-digit answer to a multiplication (product) made of a tens digit, and a units digit.
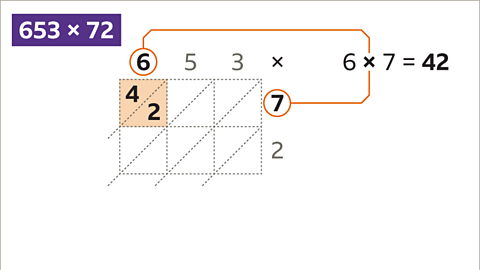
Image caption,
The highlighted cell holds the answer to the product 6 x 7. 6 x 7 is 42, 4 tens and 2 units.
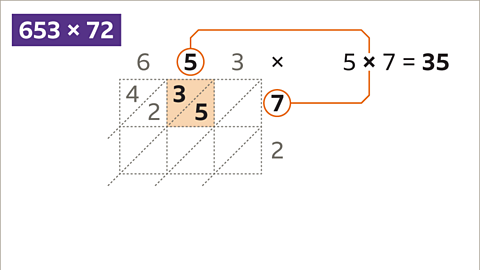
Image caption,
This cell holds the answer to the product 5 x 7. 5 x 7 is 35, 3 tens and 5 units.
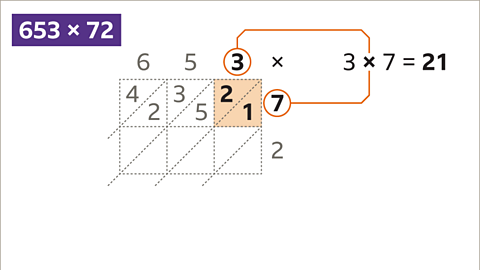
Image caption,
This cell holds the answer to the product 3 x 7. 3 x 7 is 21, 2 tens and 1 unit.
Image caption,
The second row of the grid is completed with the three products, 6 x 2, 5 x 2 and 3 x 2.
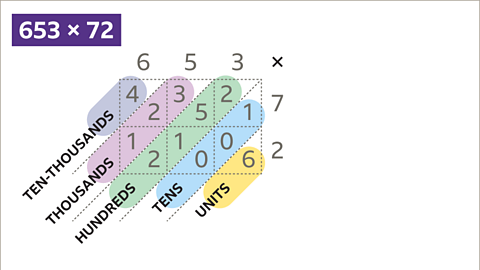
Image caption,
The grid is filled with all the products. The sum of each diagonal gives part of the final answer. From right to left, the first diagonal is the units. The second diagonal is the tens. The third diagonal is the hundreds. The fourth diagonal is the thousands. And the fifth diagonal is the ten-thousands.
Image caption,
Add up each diagonal. Remember to carry when you get a two-digit answer.
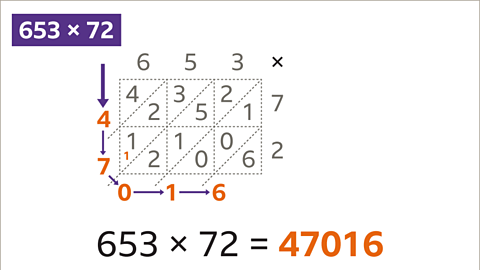
Image caption,
Follow the arrows to write the calculation with the answer: 653 x 72 = 47,016
Image caption,
Multiplication is commutative so 653 x 72 = 72 x 653. The calculation can be done on a 3 by 2 grid or a 2 by 3 grid.

Practise Napier’s method

Question: spot the mistake

The answer to this calculation is incorrect.Try to find the mistakes in the working. You might need a pen and paper.

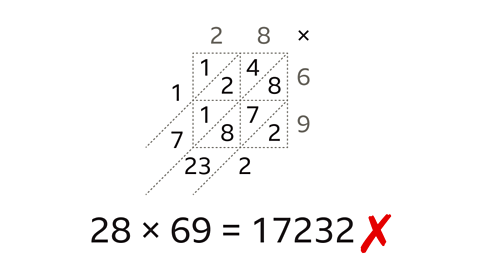
Napier grid used for the calculation twenty eight multiplied by sixty nine equals seventeen thousand, two hundred and thirty two is incorrect.

Practise: Napier’s method quiz

Practise long multiplication using Napier's method with this quiz. A pen and paper might be useful to help with your workings out.

Real-world maths

Female in a warehouse wearing a hard hat and hi-viz writing on a clipboard — Image caption,
In the workplace a calculator may not be available so working it out manually is a useful skill to have.

When you do not have a calculator, Napier’s method for long multiplication is one way of calculating your answer.

Multiplication is used to determine areas, quantities for batch production, materials needed for construction projects and much more.

It is a skill used by professionals in catering, engineering, construction and across many businesses. It can be an invaluable skill for the world of work.

How to multiply using Napier's method

Key points

How to use Napier’s method of long multiplication

Example: calculate 37 x 91

Example: calculate 653 x 72

Practise Napier’s method

Question: spot the mistake

Practise: Napier’s method quiz

Real-world maths

More on Operations - Calculations

Key points

How to use Napier’s method of long multiplication

Example: calculate 37 x 91

Example: calculate 653 x 72

Practise Napier’s method

Question: spot the mistake

Show moreShow less

Practise: Napier’s method quiz

Real-world maths

More on Operations - Calculations