Key points about formulae

A formula (formulae)A mathematical rule that links variables, by substituting the values that can be changed with words or letters, eg 𝑎² + 𝑏² = 𝑐². A formula contains an equals (=) sign. is a mathematical rule or relationship that uses words or letters to represent amounts that can be changed (variables).
Values must be substituteIn algebra, to replace a letter with a number. into formula (formulae)A mathematical rule that links variables, by substituting the values that can be changed with words or letters, eg 𝑎² + 𝑏² = 𝑐². A formula contains an equals (=) sign. using the correct order of operations (BIDMASA way to remember the correct order of operations when calculating the value of an expression. BIDMAS stands for Brackets, Indices, Division, Multiplication, Addition, Subtraction. ).
The subjectThe subject of a formula or equation is the variable on its own on one side of the equals sign, eg 𝑦 is the subject in 𝑦 = 3𝑥 + 5. of a formula can be changed so that a different variable appears at the start. This requires inverse operationThe opposite of a mathematical process. For example, the inverse of × 5 is ÷ 5. The inverse operation undoes the original process. .
Refresh your understanding of this topic by looking at this guide on calculating with negative numbers and using BIDMAS.
Check your understanding
Video – Creating formulae
Watch this video to find out how to create algebraic formulae for real-life situations, using worked examples.
Creating formulae.
An algebraic formula is a bit like an equation. It has an equals sign and variables; these are letters that represent values that can be changed. It might also have a constant, which is a number that always stays the same.
Let's look at how to create formulae for real life situations.
Vina receives £20 from her parents for her birthday. She then earns £30 each week from her Saturday job. She puts all the money she receives into a savings account.
Part A of this question asks: write a formula for the amount of money, 𝑆, in pounds, Vina will have saved after 𝑥 weeks.
To answer this, you can use a bar model where a 20 bar represents the initial £20 Vina receives from her parents and separate 30 bars represent the extra £30 Vina earns each week from her Saturday job.
So, after 1 week, Vina will have a total of £20 add £30. Then, after 2 weeks, Vina will have a total of £20 add two £30. After 3 weeks, £20 add three £30, and so on. The number of 30 bars is equal to the number of weeks. So, after 𝑥 weeks there will be 𝑥 30 bars.
The total amount of money Vina has saved is equal to the sum of all the bars. So, after 𝑥 weeks, Vina will have £20 add 𝑥 times £30, or 20 add 30𝑥. In the question, 𝑆 is used to represent this amount. So, the formula is 𝑆 equals 20 add 30𝑥.
Part B of the question asks you to work out how much money, in pounds, Vina would have saved after 12 weeks.
𝑥 represents the number of weeks. So, substitute 𝑥 equals 12 into the formula. 30 times 12 is 360 and 360 add 20 is 380. So, Vina will have saved £380 after 12 weeks.
Let's look at another question.
Bruno adds £56 to his travel card. Every day he buys a £2 bus ticket using this money. Write a formula for how much money, 𝑀, in pounds, Bruno has left on his travel card after 𝑥 days.
Pause the video and have a go.
Be careful here. This time, the amount he’s spending has been taken away from the initial £56.
Starting with a 56 bar, after 1 day, Bruno will have 56 subtract 1 times £2, which is £54. Then, after 2 days he will have 56 subtract 2 times £2, or £52. After 3 days, 56 subtract 3 times £2, or £50, and so on. So, after 𝑥 days, he will have 56 subtract £2𝑥 left.
𝑀 is how much money Bruno has left. So, the formula is 𝑀 equals 56 subtract 2𝑥.
Writing formulae
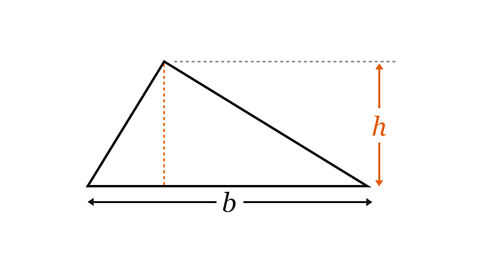
Formulae are used in many areas of maths and science, eg for finding the area of a shape or for calculating speed.
Formulae are also helpful in everyday life, for example working out the time needed to cook something according to its weight - if we know certain values we can create a formula to work out an unknown.
For example, the formula to work out the area of a triangle, 𝑨, in terms of its base, 𝒃, and its height, 𝒉, is:
𝑨 = \(\frac{bh}{2}\)
𝑨 is the subjectThe subject of a formula or equation is the variable on its own on one side of the equals sign, eg 𝑦 is the subject in 𝑦 = 3𝑥 + 5. of the formula. 𝒃 and 𝒉 are variableA quantity that can take on a range of values, often represented by a letter, eg 𝑛, 𝑥, 𝑦, 𝑧, 𝑡 … etc. because they can change depending on the values of the base and height. To calculate the area, substituteIn algebra, to replace a letter with a number. 𝒃 and 𝒉 with values.
Follow the working out below
GCSE exam-style questions
- A taxi company charges a one-off charge of £6.50, and then 95p per mile.
Write a formula for 𝐶, the total cost of a journey in £, in terms of the number of miles, 𝑚.

𝑪 = 6·5 + 0·95𝒎
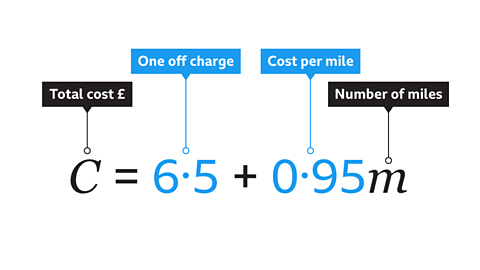
The units must all be in pounds. The total cost in pounds, 𝐶, is equal to the one-off charge plus £0.95 for each mile.
£6.50 can be written as 6·5. There is no need to write the £ symbol in the formula because 𝐶 is the cost in pounds.
Remember to include “𝐶 =”. A formula must have a subject and an equals sign.
- A factory fills cat litter into different sized bags. Each bag contains 800 g, 1·4 kg or 2 kg.
Write a formula for 𝑇, the total mass of the cat litter filled in kg, in terms of the number of small bags (𝑠), medium bags (𝑚) and large (𝑙) bags.

𝑻 = 0·8𝒔 + 1·4𝒎 + 2𝒍
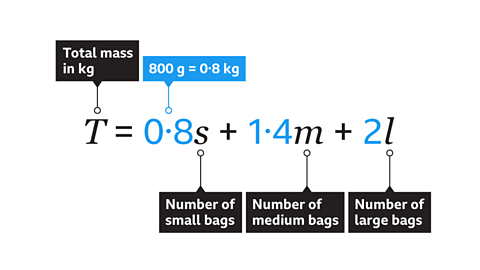
The mass of all the small bags is the number of small bags multiplied by 0·8, and similarly for the medium and large bags.
The total mass, 𝑇, is equal to the three expressions added together.
The formula must include “𝑇 =” at the start.
Substituting into expressions and formulae

An expression is a mathematical sentence expressed either numerically or symbolically, made up of one or more term (algebra)An element within an algebraic sentence, eg 𝑥 or 5𝑦 or 3𝑒². Elements (terms) are separated by + or – signs..
A formula is a mathematical rule or relationship that uses words or letters to represent amounts that can be changed, known as variables.
Substitution means putting numbers in place of letters to calculate the value of an expressionA mathematical sentence expressed either numerically or symbolically made up of one or more terms, eg 8 + 2, or 6𝑥, or 5𝑥² + 3𝑦, or 3𝑎𝑏𝑐. . The expression could be part of a formula (formulae)A mathematical rule that links variables, by substituting the values that can be changed with words or letters, eg 𝑎² + 𝑏² = 𝑐². A formula contains an equals (=) sign..
The correct order of operations, BIDMAS or BODMASAn acronym listing the order in which each part of a calculation must be worked out. Brackets, Indices (or pOwers), Division and Multiplication, and Addition and Subtraction. (or BODMAS), must be followed.
For example, values containing indicesIndices are powers. For example, 3 to the power of 2, written 3². The singular for indices is 'index'. must be worked out before multiplication.

Follow the working out below
GCSE exam-style questions
- Find the value of this expression when 𝑥 = –5.
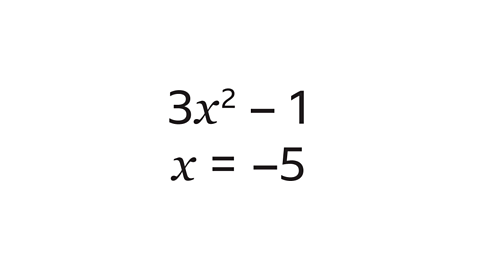
74

Substitute –5 in place of 𝑥.
Put a bracket around –5 to show it is –5 being squared and not just 5.
3. Follow BIDMAS and calculate the value with indices first:
–5 × –5 = 25, so replace (–5)² with 25.
Next do the multiplication. Replace 3 × 25 with 75.
Then do the subtraction to get 74.
- This formula is used to convert Celsius (𝐶) to Fahrenheit (𝐹).
What is the temperature in Fahrenheit if it is 20°C?
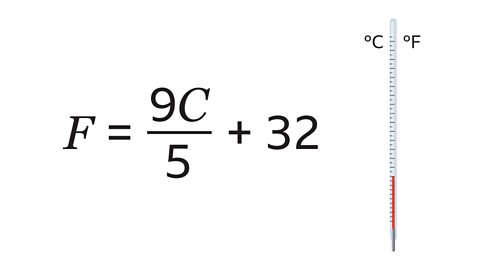
68°F
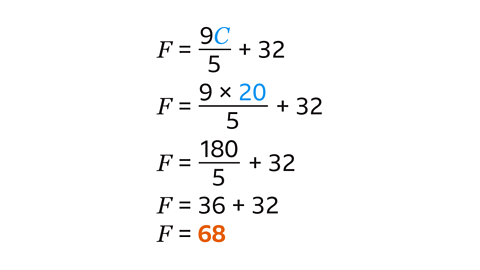
Substitute 20 in place of 𝐶 in the formula.
Calculate the value of the top of the fraction first:
- 9 × 20 = 180.
The fraction line means ‘divided by’ so divide the answer by 5:
- 180 ÷ 5 = 36.
Finally, do the addition. Add 32 to your answer to get 𝐹 = 68. The formula says that when the temperature in Celsius is 20°C, it is 68°F in Fahrenheit.
Video - Exam practice: Creating algebraic formulae
Watch this video to learn how to create algebraic formulae and find out how they can help you in real-life situations.
While studying for your exams, have you ever wondered, 'how will algebra and formulae ever help me in real life?' Here's how they can be useful.
Let's say your favourite band are performing at a concert you want to go to with your friends. Booking online tickets cost £25, and merch t-shirts cost £10 each. There is also a £5 admin fee, no matter how many tickets and t-shirts you order.
How much money do you need to buy four tickets and three t-shirts for you and your friends? You can create a formula to help you calculate this. The total cost we are trying to work out is C. The admin fee is £5 and that's a fixed cost, no matter what. So, that's the constant.
The tickets and t-shirts have a fixed cost, but the number you can buy can change. These changing values are called the variables. We'll call the number of tickets, 𝑥, and the number of t-shirts, 𝑦. Each ticket costs £25, so that's why we add on 25𝑥 to the formula.
Then t-shirts cost £10 each, so we add on 10𝑦. Our formula is C = 5 + 25𝑥 + 10𝑦. We want 4 tickets, so the variable, 𝑥 = 4. And we want 3 t-shirts, so the variable, 𝑦, is 3.
So, C = 5 + (25 × 4) + (10 × 3). The total money you'll need is C = 5 + 100 + 30, which equals £135.
Maybe you're going with 7 friends and have £250 between you. Once you've paid for the tickets and the admin fee, how many of you can buy t-shirts? Let's use our formula, C = 5 + 25𝑥 + 10𝑦 to model this new situation.
We know that we have £250 to spend, so we need to replace the C in our formula with 250. We can also replace the variable, 𝑥, with the number of tickets we need, which is 8, including your own ticket. So, our formula is now 250 = 5 + 25 × 8 + 10𝑦, which is 250 = 205 + 10𝑦.
To find the number of t-shirts we can buy, we need to work out what 𝑦 equals.
First, we subtract 205 from both sides to give 45 = 10𝑦. Then, divide both sides by 10 to get 𝑦 = 4.5. This means you can buy four t-shirts and have a little bit of money left over.
So, formulae aren't just for the classroom. Putting them to use in real life can help you make smart decisions when it comes to things you enjoy.
Changing the subject of a formula
The subject of a formula is the variableA quantity that can take on a range of values, often represented by a letter, eg 𝑛, 𝑥, 𝑦, 𝑧, 𝑡 … etc. on its own on one side of the equals sign.
In the case of 𝑦 = 3𝑥 + 4, 𝑦 is the subject.
To change the subject of a formula, the termAn element within an algebraic sentence, eg 𝑥 or 5𝑦 or 3𝑒². can be rearranged so that a different variableA quantity that can take on a range of values, often represented by a letter, eg 𝑛, 𝑥, 𝑦, 𝑧, 𝑡 … etc. is on its own.
To help rearrange a formula, it can be helpful to draw a function machineUsed to present each step of a function visually. A function machine takes an input, performs certain operations, and gives out an output. that shows each step of the formula.
From that, the reverse of the function machine can be worked out. The reverse steps show the inverseThe opposite of a mathematical process. For example, the inverse of × 5 is ÷ 5. The inverse process undoes the original process. and are needed to rearrange the formula.
The process is similar to solving equations.
The following are common inverse operations:
Follow the working out below
GCSE exam-style questions

- Rearrange this formula to make 𝑒 the subject.
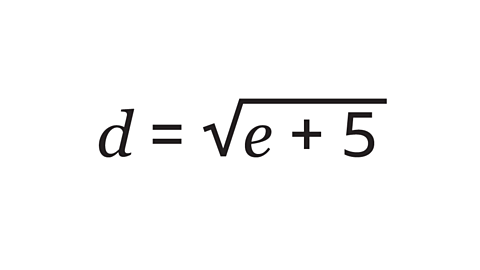
𝑒 = 𝑑² − 5
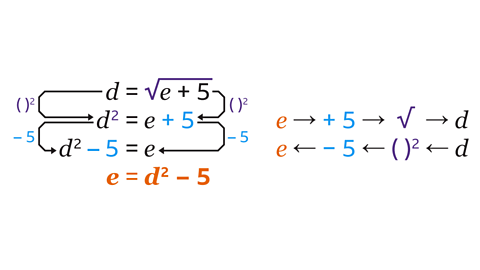
This function machine is a two-step process: add 5 and then square root. To rearrange the formula, these steps are undone by completing them in reverse order using the inverse operations.
The inverse of square rooting is squaring. Square both sides. The formula is now 𝑑² = 𝑒 + 5
The inverse of add 5 is subtract 5. Subtract 5 from both sides. The formula is now 𝑑² − 5 = 𝑒
𝑒 has been isolated and is now the subject of the formula.
- Rearrange the formula for the area of a circle to make the radius the subject.
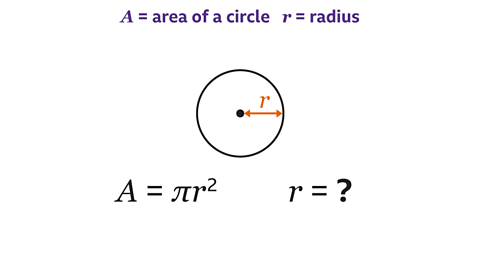
𝑟 = \(\sqrt \frac{A}{π}\).
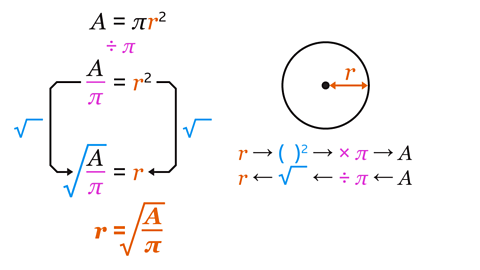
The function machine is a two-step process: square and then multiply by π. To rearrange the formula, these steps are undone by completing the steps in reverse order using the inverse operations.
The inverse of multiply by π is divide by π. Divide both sides of the formula by π. The formula is now \(\frac{A}{π}\) = 𝑟².
The inverse of squaring is square rooting. Square root both sides of the formula. Be sure to square root the whole expression. The formula is now \(\sqrt \frac{A}{π}\) = 𝑟.
𝑟 has been isolated and is now the subject of the formula.
- This formula is used to convert Celsius (𝐶) to Fahrenheit (𝐹). Make 𝐶 the subject so that the formula converts Fahrenheit to Celsius.
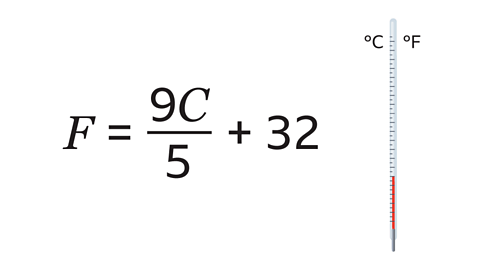
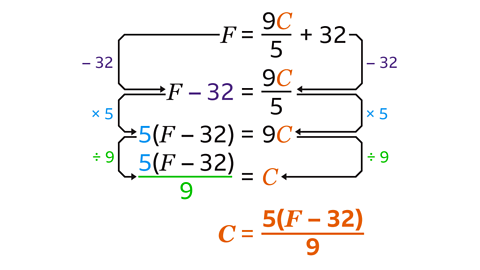
The function machine is a three-step process: multiply by 9, divide by 5 and then add 32. To rearrange the formula, these steps are undone using the inverse operations:
The inverse of add 32 is subtract 32. Subtract 32 from both sides of the formula.
The inverse of divide by 5 is multiply by 5. Multiply both sides by 5.
The inverse of multiply by 9 is divide by 9. Divide both sides by 9.
𝐶 has now been isolated and is the subject of the formula.
Quiz - Formulae
Practise what you've learned about formulae with this quiz.
Higher - Changing the subject of a formula where subject appears twice
When rearranging formulae to change the subjectThe subject of a formula or equation is the variable on its own on one side of the equals sign, eg 𝑦 is the subject in 𝑦 = 3𝑥 + 5. to a different variable, sometimes this variable appears more than once.
The terms that contain the subject need to be collected on one side of the equals sign.
To do this, the expression can be factoriseTo express a number or an expression as the product of its factors, eg 6 can be factorised as 2 × 3, and 6𝑛 – 12 can be factorised as 6(𝑛 – 2). so the subject is outside the bracket.
The subject can then be isolated by dividing both sides by the bracket.
Follow the working out below
Higher – Video – Rearranging equations with fractions
Watch this video to find out how to rearrange equations where the subject appears twice, using fractions.
Rearranging equations with fractions – Higher tier.
It is sometimes useful to rearrange equations or formulae to make a different variable the subject. Remember, variables are letters that represent values that can be changed.
For example, the area of a rectangle is given by the length times the width. You can substitute known length and width values into this formula to calculate the area. But what if you know the area and length but not the width? Then, it would be useful to have the formula in the form 𝑤 equals, where 𝑤 is now the subject. To make 𝑤 the subject, you would need to divide both sides of the equation by 𝑙.
Remember, all equations have an equals sign, which means they need to be balanced like a set of scales.
So, you must divide both sides by 𝑙, giving 𝐴 over 𝑙 equals 𝑙𝑤 over 𝑙. On the right-hand side, 𝑙 cancels out. Leaving 𝐴 over 𝑙 equals 𝑤, which you can rewrite as 𝑤 equals 𝐴 over 𝑙.
This process is called rearranging. Let's look at an example question.
Make 𝑥 the subject of 𝑦 equals 2𝑥 subtract 5, all over 𝑥.
To do this, you need to rearrange the equation so that it's in the form 𝑥 equals instead of 𝑦 equals. In its current form, the equation is tricky to work with. So, let's start by addressing the fraction part.
2𝑥 subtract 5 is divided by 𝑥, so to remove the fraction you need to use the inverse operation, which is multiplying by 𝑥. The left-hand side simplifies to 𝑥𝑦 and on the right-hand side, multiplying by 𝑥 cancels with the denominator. So, the equation becomes 𝑥𝑦 equals 2𝑥 subtract 5.
The next step is to get all the 𝑥 terms on one side of the equation, and all the non-𝑥 terms on the other side. To do this, subtract 2𝑥 from both sides, giving 𝑥𝑦 subtract 2𝑥 equals 2𝑥 subtract 5 subtract 2𝑥.
2𝑥 subtract 2𝑥 equals 0, so this gives 𝑥𝑦 subtract 2𝑥 equals –5. Then, 𝑥𝑦 and –2𝑥 both have a common factor of 𝑥 which means you can factorise the left-hand side or in other words, put the expression into brackets. Taking out the factor of 𝑥 gives 𝑥 all multiplied by 𝑦 subtract 2 equals negative five. The 𝑥 is now on its own outside the bracket, so you're nearly there.
To finish and get 𝑥 completely on its own on the left-hand side, you need to use the opposite operation to multiplying by 𝑦 subtract 2 which is dividing by 𝑦 subtract 2. 𝑦 subtract 2 cancels on the left-hand side, so you have 𝑥 equals –5 all over 𝑦 subtract 2, where 𝑥 is now the subject.
GCSE exam-style questions
- This is the formula for the surface area of a closed box, 𝐴. Rearrange the formula to make 𝑏 the subject.

𝑏 = \(\frac{A − 2wh}{2w + 2h} \)
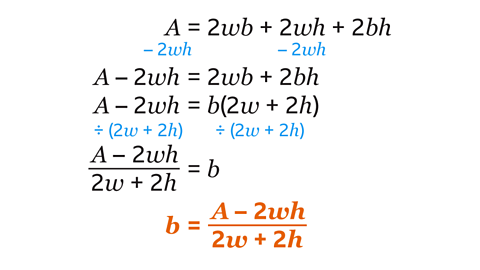
Subtract 2𝑤ℎ from both sides. Now the right-hand side has terms that only contain the required subject, 𝑏.
- 𝐴 – 2𝑤ℎ = 2𝑤𝑏 + 2𝑏ℎ.
factoriseTo express a number or an expression as the product of its factors, eg 6 can be factorised as 2 × 3, and 6𝑛 – 12 can be factorised as 6(𝑛 – 2). the right-hand side by putting 𝑏 on the outside of the bracket. There is no need to take 2 out of the bracket as well.
- 𝐴 – 2𝑤ℎ = b(2𝑤 + 2ℎ).
Divide by the bracket to isolate 𝑏.
- 𝑏 is now on its own as the subject of the formula.
- Rearrange this formula to make 𝑥 the subject.
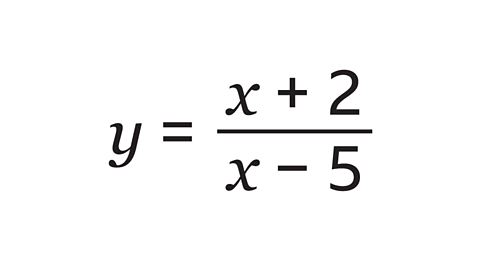
𝑥 = \(\frac{2 + 5y}{y − 1} \)
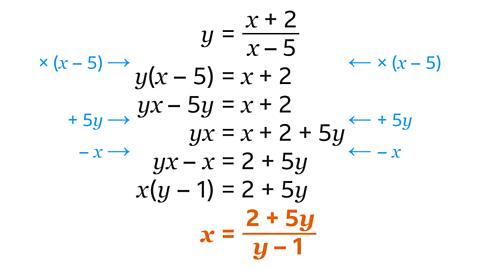
Multiply both sides by (𝑥 – 5) to remove the fraction.
- 𝑦 (𝑥 – 5) = 𝑥 + 2
Expand the bracket.
- 𝑦𝑥 – 5𝑦 = 𝑥 + 2
Add 5y to both sides.
- 𝑦𝑥 = 𝑥 + 2 + 5𝑦
Subtract 𝑥 from both sides.
- 𝑦𝑥 – 𝑥 = 2 + 5𝑦
Now all the terms containing 𝑥 are on one side.
Factorise to take 𝑥 out of the bracket.
- 𝑥(𝑦 – 1) = 2 + 5𝑦
Finally, divide both sides by (𝑦 – 1) make 𝑥 the subject.
Now that you have revised formulae, why not try looking at this guide on inequalities?
More on Algebra
Find out more by working through a topic
- count5 of 14
- count6 of 14

- count7 of 14

- count8 of 14