Key points about sequences
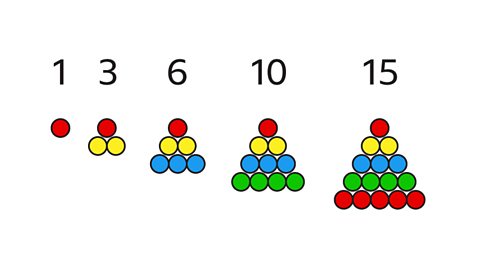
A number sequence is a list of ordered numbers that follow a pattern or a rule. A term-to-term rule explains how to find the next A value in a sequence. The 3rd term is the 3rd value in the sequence. of a sequence.
The 𝑛th term of a sequence is a position-to-term rule that can be used to find out any term in a sequence.
The 𝑛th term of an A sequence that increases or decreases by the same number each time, eg 4, 7, 10, 13. Sometimes called a linear sequence. (sometimes known as a linear sequence) is found by comparing the sequence to an appropriate times table.
Higher tier - The 𝑛th term of a Describing an expression of the form 𝑎𝑥² + 𝑏𝑥 + 𝑐 where 𝑎, 𝑏 and 𝑐 are integers. sequence is found by considering the Once the first difference between values of a sequence is calculated, the second difference is the difference between these values. between the terms and comparing the sequence to another that contains 𝑛².
Check your understanding
Term-to-term rules
A sequence is a list of values that follow a rule. Each value is called a term.
A rule that explains how to find the next term in a sequence is called a term-to-term rule.
The most common type of sequence is an arithmetic (or linear) sequence. The difference between each term is the same every time, and is known as the common difference.
Follow the working out below
GCSE exam-style questions
- –20, –17, –14, –11 are the first four terms of a sequence. Find the term-to-term rule.
The term-to-term rule is ‘add 3’.
The negative numbers are getting closer to zero and the terms are increasing by 3 each time.
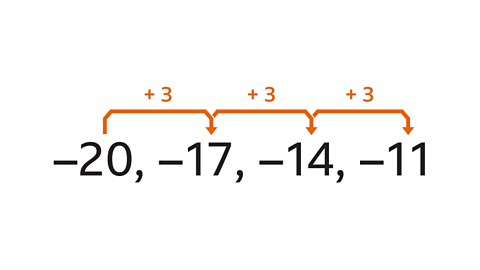
- The term-to-term rule of a sequence is ‘multiply by 5, then subtract 3’. The first term is 2. Work out the 3rd term.
The third term is 32
To work out the second term, multiply the first term by 5, then subtract 3.
2 × 5 – 3 = 7.
To work out the third term, multiply the second term by 5, then subtract 3.
7 × 5 – 3 = 32.
- The term-to-term rule of a sequence is ‘add 3 then multiply by 2’. The third term is 46. Calculate the first term.
The first term is 7.
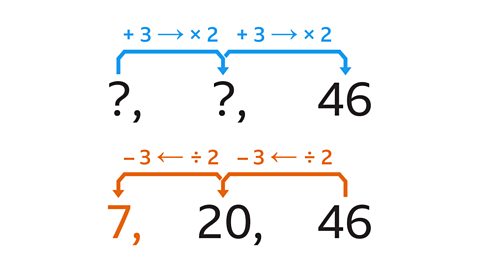
- To calculate the second term, work backwards from the third term. The term-to-term rule in reverse is ‘divide by 2, then subtract 3.’
46 ÷ 2 = 23. Then 23 – 3 = 20. The second term is 20.
- To calculate the first term, work backwards from the second term. Use the same term-to-term rule in reverse.
20 ÷ 2 = 10. Then 10 – 3 = 7. The first term is 7.
𝒏th term rules
Rather than finding the next term or next two terms of a sequence, it may be necessary to work out the 50th term, for example.
To do this without writing out all 50 terms, a general rule called the 𝒏th term is found.
To find an A mathematical sentence expressed either numerically or symbolically made up of one or more terms, eg 8 + 2, or 6𝑥, or 5𝑥² + 3𝑦, or 3𝑎𝑏𝑐. for the 𝑛th term of an A sequence that increases or decreases by the same number each time, eg 4, 7, 10, 13. Sometimes called a linear sequence. , work out the The difference between each term in an arithmetic linear sequence. between the terms and treat the sequence as a times table that has been shifted.
- For example, 3, 7, 11, 14 has a common difference of 4, and is the 4 times table with 1 subtracted. The 𝑛th term is therefore 4𝑛 – 1.
To find the 50th term, In algebra, to replace a letter with a number. the value of 50 into the 𝑛th term rule.
Follow the working out below
GCSE exam-style questions
- A linear sequence starts 3, 8, 13, 18, 23. Work out an expression for the 𝑛th term.
5𝑛 – 2
Write the numbers for 𝑛 above the sequence.
The common difference between the terms is 5, so write the 5 times table under Click here to enter text. the values of 𝑛. Label the 5 times table as 5𝑛.
Work out how to get from the 5𝑛 row to the sequence. The sequence is the 5 times table subtract 2. The 𝑛th term is 5𝑛 – 2.
- An arithmetic sequence starts 14, 11, 8, 5, 2. Work out an expression for the 𝑛th term.
–3𝒏 + 17
- Write the numbers for 𝑛 above the sequence.
- The common difference is –3, so write the –3 “times table” under the values of 𝑛. Label the row as –3𝑛.
- Work out how to get from the –3𝑛 row to the sequence. The –3𝑛 row has had 17 added.
The 𝑛th term is –3𝑛 + 17.
(Another way to write the answer is 17 – 3𝑛).
- Write down the first three terms of a sequence where the 𝑛th term is given by 𝑛² + 5.
6, 9, 14
1. The first term is when 𝑛 = 1. Substitute 1 into 𝑛² + 5 to give 12 + 5 = 6.
- The second term is when 𝑛 = 2. Substitute 2 into 𝑛² + 5 to give 22 + 5 = 9.
3. The third term is when 𝑛 = 3. Substitute 3 into 𝑛² + 5 to give 32 + 5 = 14.
4. The first three terms are 6, 9, 14.
(Note: this sequence is not an arithmetic sequence as it does not go up by the same number each time.)
Quiz – Sequences
Practise what you have learned about sequences with this quiz.
Higher – 𝒏th term of a quadratic sequence
Quadratic sequences have an 𝑛th term rule that contains 𝑛².
Follow the working out below
Example 1
Example 2
The differences between the terms are not equal, but the Once the first difference between values of a sequence is calculated, the second difference is the difference between these values. between the terms are equal.
To find the 𝑛th term, follow these steps:
Work out the first differences between the terms. The first differences are not the same. Work out the second differences.
The second differences will be the same. The A number or symbol multiplied with a variable or an unknown quantity in an algebraic term. For example, 4 is the coefficient of 4n². (𝑎) of 𝑛² in the 𝑛th term rule is always half of the second difference.
Compare the numbers of the sequence 𝑎𝑛² with the original quadratic sequence. The difference between them will be a A number that does not vary. Constants are different to variables such as 𝑥 and 𝑦 that can take many values. , or should make an A sequence that increases or decreases by the same number each time, eg 4, 7, 10, 13. Sometimes called a linear sequence. .
Add the constant or 𝑛th term for the arithmetic sequence to 𝑎𝑛² to give the 𝑛th term for the quadratic sequence.
GCSE exam-style questions
- A quadratic sequence has an 𝑛th term of 2𝑛² + 4𝑛 – 3. Find the first 3 terms.
3, 13, 27
Substitute 𝑛 = 1 into the expression. The first term is 2(1²) + 4(1) – 3 = 2(1) + 4 – 3 = 3
Substitute 𝑛 = 2 into the expression. The second term is 2(2²) + 4(2) – 3 = 2(4) + 8 – 3 = 13
Substitute 𝑛 = 3 into the expression. The third term is 2(3²) + 4(3) – 3 = 2(9) + 12 – 3 = 27
- Work out the 𝑛th term of the sequence 6, 9, 14, 21, 30.
𝒏² + 5
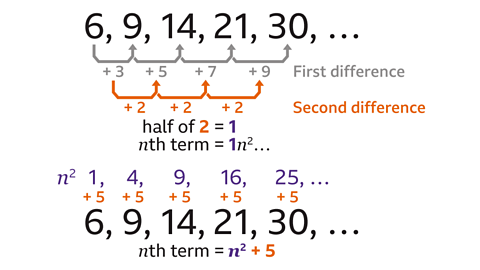
The first differences are + 3, + 5, + 7, + 9.
The second differences are all +2. Half of 2 is 1, so the coefficient of 𝑛² is 1.
Write the values of 1𝑛² and compare it to the sequence. The constant value of 5 is always added to 𝑛² to make the sequence.
Write the final 𝑛th term rule as 𝑛² + 5.
- Work out the 𝑛th term of the sequence 3, 9, 17, 27, 39.
𝑛² + 3𝑛 – 1
The first differences are + 6, + 8, + 10, + 12.
The second differences are all + 2. Half of 2 is 1, so the coefficient of 𝑛² is 1.
Write the values of 1𝑛² and compare it to the sequence. The differences 2, 5, 8, 11, 14 form an arithmetic sequence whose 𝑛th term is 3𝑛 –1 (the 3 times table subtract 1).
Add 3𝑛 – 1 to 𝑛² to give the final 𝑛th term rule
𝑛² + 3𝑛 – 1.
Quadratic sequences – interactive activity
This interactive activity will help you to learn how to create quadratic sequences by selecting different coefficient values.
Higher – Quiz – Sequences
Practise what you have learned about sequences with this quiz for Higher tier.
Now that you have revised sequences, why not try looking at geometric and special sequences?
More on Algebra
Find out more by working through a topic
- count11 of 14
- count12 of 14
- count14 of 14
