Key points about negative and fractional indices
The notation in which a product such as 𝑛 × 𝑛 × 𝑛 × 𝑛 is recorded as 𝑛⁴. In this example the number 4 is called the index (plural indices) and the number represented by 𝑛 is the base. condenses a calculation.
This is when a The number or variable that is raised to a power when using index notation. (number or A quantity that can take on a range of values, often represented by a letter, eg 𝑛, 𝑥, 𝑦, 𝑧, 𝑡 … etc. ) is raised to a A number that is multiplied by itself one or more times is raised to a power. 𝑛⁴ is ‘𝑛 to the power of 4’ and means 𝑛 × 𝑛 × 𝑛 × 𝑛. The power is the value of the index or exponent..The Agreed rules for simplifying expressions (involving multiplication, division and raising to a power) using index notation with the same base. are rules for To make an expression shorter by collecting terms of the same kind. A mathematical sentence expressed either numerically or symbolically made up of one or more terms, eg 8 + 2, or 6𝑥, or 5𝑥² + 3𝑦, or 3𝑎𝑏𝑐. involving powers with the same base. The indices may be positive or negative Integers are numbers with no fraction or decimal part. They can be positive, negative or zero. 42, –8, and 10,000 are examples of integers. or fractional values.
Any base to the power of zero equals 1 and any base to the power of one is the base itself.
Look at these guides on the laws of indices and powers to support your confidence in this topic.
Video – Negative indices
Watch this video to learn how to use the laws of indices when working with negative indices.
Negative indices.
Laws of indices are helpful for understanding and working out negative indices.
Consider these powers of 2: 2 is simply 2 to the power of 1, 4 is 2 squared, 8 is 2 cubed, and 16 is 2 to the power of 4.
Notice if you multiply by 2, the powers increase and if you divide by 2, the powers decrease.
But what if you keep going to the power of zero and even smaller?
2 to the power of zero is 1, 2 to the negative 1 is 1 over 2 to the power of 1, which equals one half, 2 to the negative 2 is 1 over 2 squared, or one quarter, and so on.
Notice that the values obtained by raising numbers to negative indices, are the same as the values obtained raising the same numbers to positive indices but flipped.
In other words, they're reciprocals.
This is true for all negative indices. Any number or variable with a negative index, can be written as 1 over that number or variable, to the equivalent positive index.
So, for example, x to the negative 4 equals 1 over x to the 4, 2x to the negative 3 equals 2 over x to the 3, and 2x all to the negative 7 equals 1 over 2x all to the 7.
Let's see how this relates to the laws of indices:
x to the 4, multiplied by x to the negative 2. Remembering the rule for negative indices: x to the negative 2 is the same as 1 over x squared. This can be written out, in full, as a fraction with four ‘x’s multiplied together as the numerator, and two ‘x’s multiplied together as the denominator. Then, cancelling down ‘x’s gives x squared.
Using the index law for multiplication, the calculation simplifies to x to the 4 add negative 2, which equals x squared, just like before.
How about x to the 4 divided by x to the negative 2?
This can be written as four ‘x’s multiplied together, divided by 1 over two ‘x’s multiplied together.
Dividing by a fraction is the same as multiplying by its reciprocal. So, this is six ‘x’s multiplied together, or x to the 6.
Using the index law for division, the calculation simplifies to x to the 4 subtract negative 2. Which again equals x to the 6.
And finally, let's look at x to the 4, all to the power of negative 2.
This can be written as 1 over x to the four, all squared.
Writing this out in full gives 1 over x multiplied by itself 8 times, which is 1 over x to the 8, or x to the power of negative 8.
Let’s work this out using the index law for powers of powers.
The calculation simplifies to x to the 4 times negative 2, which also equals x to the negative 8.
Letters or numbers to the power of zero
A base may be a variable or a number.
A base to the power of zero is equal to one:
- 𝑎\(^0\) = 1
- 3\(^0\) = 1
A term divided by itself is equal to one:
- 𝑛\(^4\) ÷ 𝑛\(^4\) = 1
- 5 ÷ 5 = 1
A base to the power of one is equal to the base itself:
- 𝑎\(^1\) = 𝑎
- 8\(^1\) = 8
Follow the working out below
GCSE exam-style questions
- What is the value of 𝑥?
6\(^𝑥\) = 1
𝑥 = 0
A base to the power of zero is equal to 1.
- 6\(^𝑥\) = 1
- 6\(^0\) = 1
- 𝑥 = 0
- Simplify the expression.
𝑦\(^9\) ÷ (𝑦\(^2\) )\(^4\)
𝑦\(^1\) = 𝑦
Simplify the term raised to a power, multiply the indices:
- (𝑦\(^2\))\(^4\) = 𝑦\(^8\)
Simplify 𝑦\(^9\) ÷ 𝑦\(^8\) by subtracting the indices:
- 𝑦\(^9\) 𝑦\(^8\) = 𝑦\(^1\)
A base to the power of one is the base itself:
- 𝑦\(^1\) = 𝑦
What are negative indices?
- A negative The notation in which a product such as 𝑛 × 𝑛 × 𝑛 × 𝑛 is recorded as 𝑛⁴. In this example the number 4 is called the index (plural indices) and the number represented by 𝑛 is the base. represents a Written as 1 divided by the number, eg the reciprocal of 2 is ½ and the reciprocal of ½ is 2. The reciprocal is also called the multiplicative inverse. Any non-zero number multiplied by its reciprocal is equal to one.:
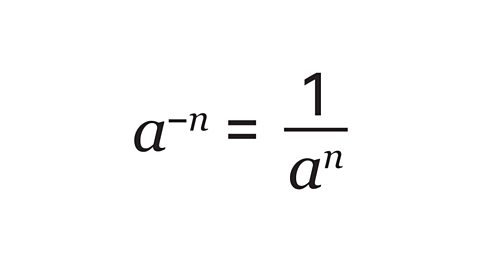
- A term and its reciprocal have a product of 1:
Follow the working out below
GCSE exam-style questions
- Write this term with a positive index: 𝑝\(^-\)\(^4\).
'𝑝 to the power of negative four' is the reciprocal of '𝑝 to the power of 4'.
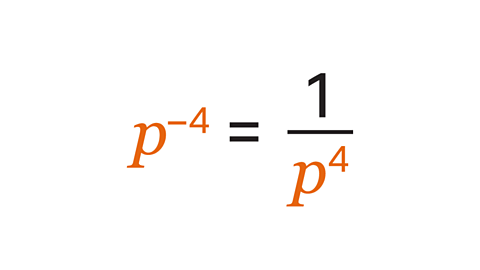
Therefore, the answer is: one divided by 𝑝 to the power of 4.
- Find the exact value of 5\(^–\)\(^3\).
5\(^–\)\(^3\) = \(\frac{1}{125}\) (as a decimal this is 0·008).
The negative index gives the reciprocal of five cubed.
5\(^3\) = 125
Check your understanding
Higher - What are fractional indices?
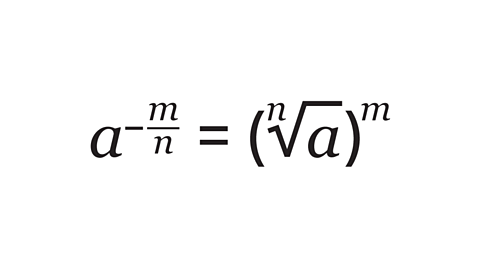
A fractional Positioned above and to the right of a number. It is an abbreviation of repeated multiplication, eg 7³ means 7 × 7 × 7. An index may be positive, negative, zero or fractional. Indices are also referred to as powers or exponents. has a Number written on the bottom of a fraction. The denominator is the number of equal parts, eg for ⅓, the denominator is 3. and a Number written at the top of a fraction. The numerator is the number of parts used, eg for ⅓, the numerator is 1.:
- The denominator represents a root.
- 2 gives a square root.
- 3 gives a cube root.
- 4 gives the fourth root and so on.
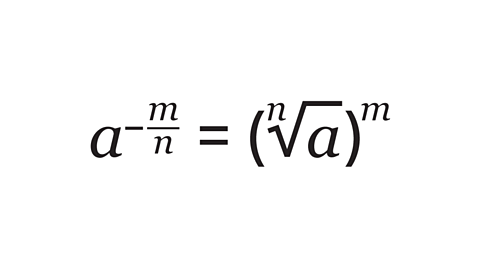
- The numerator represents a power.
- 2 gives a square.
- 3 gives a cube.
- 4 gives the fourth power and so on.
Generally, it is simpler to evaluate the root and then the power.
![a-^m/n=1/[(n&a)]^m](https://ichef.bbci.co.uk/images/ic/480xn/p0k0wcwv.png)
A negative fractional index is the Written as 1 divided by the number, eg the reciprocal of 2 is ½ and the reciprocal of ½ is 2. The reciprocal is also called the multiplicative inverse. Any non-zero number multiplied by its reciprocal is equal to one. of the positive fractional index.
Follow the working out below
GCSE exam-style questions
- Evaluate:
9
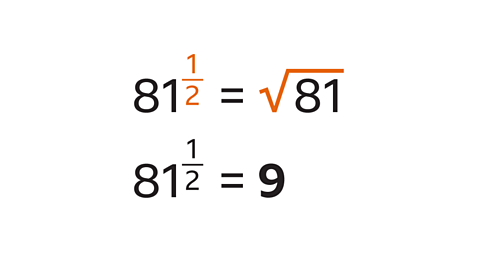
81 to the power of a half is the square root of 81.
The square root of 81 is 9.
- Evaluate:
125
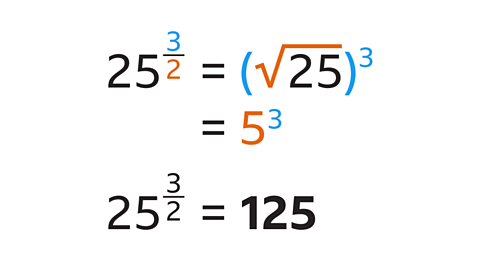
The denominator (2) indicates that you need to find the square root of the base (25). The square root of 25 is 5.
The numerator (3) indicates that you need to cube the value.
5 cubed is 5 × 5 × 5 = 125.
25 to the power of \(\frac{3}{2}\) is 125.
Now that you have revised negative and fractional indices, why not look at multiples and factors?
More on Number
Find out more by working through a topic
- count14 of 15
- count15 of 15
- count1 of 15
- count2 of 15
