Key points about whole numbers

- Use place valueThe value of a digit that relates to its position or place in a number, eg in 1482 the digits represent 1 thousand, 4 hundreds, 8 tens and 2 ones. to compare and order whole numbers.
- Numbers lined up by place value and written one underneath the other can be added or subtracted.
- Times table skills are useful when multiplying and dividing whole numbers.
Refresh your knowledge with these guides on place value and calculations with whole numbers.
Check your understanding
How to write whole numbers in words
To write a whole number in words:
- Use commas to split the number into groups of three digits from right to left.
- Read the number from left to right:
- Read each set of three digits, followed by the place value name of the group of digits.
To write a whole number in figures:
- Write each separately named number.
- Add up the numbers.
Follow the working out below
GCSE exam-style questions

- The number 92,570 is multiplied by one hundred.
Write the resulting number in words.

92,570 multiplied by 100 is 9,257,000.
Written in words, this is: Nine million, two hundred and fifty-seven thousand.
- Write the number 30,040,607 in words.
30,040,607 can be written as thirty million, forty thousand, six hundred and seven.

- Write the number ten million, four hundred and fifty thousand and seven in figures.
Ten million four hundred and fifty thousand is written 10,450,007.
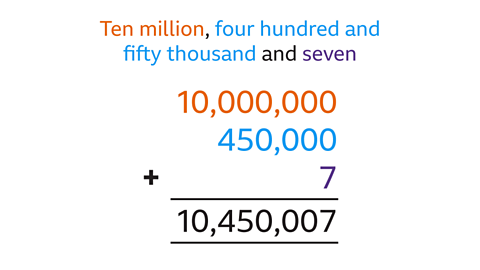
Split the words into the number of millions, thousands and hundreds, tens and units then add up the numbers.
How to order whole numbers
Whole numbers are ordered using place value.
- ascendingArranged from least value to greatest value, eg 1, 2, 3. order means start with the smallest value.
- descendingArranged from greatest value to least value, eg 3, 2, 1. order means start with the largest value.
To order whole numbers:
- Write the numbers one underneath the other, lining up the units place value digits.
- Start on the left to compare digits.
- The greater the digit, the larger the number.
- If the digits are equal, move one place to the right and compare digits again.
inequality symbols (< >)The symbol > is used when a value is greater than another, eg 23 > 5. The symbol < is used when a value is less than another, eg 11 < 40. are used to show whether a number is greater or smaller than another:
- > means greater than.
- < means less than.
Follow the working out below
GCSE exam-style questions
- Write the numbers 245, 264, 314, 257 and 265 in ascending order.
In ascending order, the numbers are: 245, 257, 264, 265, 314.

- Write the numbers one under another lining up the units digits.
- Work from the left comparing digits.
- 3 is larger than 2. 314 is the largest number.
- Move one column to the right and compare digits.
- 6 is larger than 5 and 4. 264 and 265 are greater than 245 and 257.
- 245 is the smallest number.
- 257 is the second smallest.
- Move one column to the right and compare digits the final digits of 264 and 265.
- 5 is greater than 4, so 265 is greater than 264.
- Use the correct inequality symbol to compare 19,999 and 2000.
19,999 > 2000
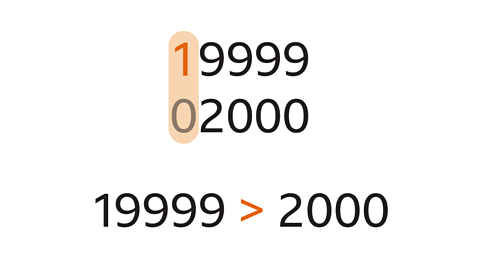
- Write the numbers one under another lining up the units digits and compare the digits from the left.
- The first digit for 19999 is 1, this is greater than the digit for 2000 as there is no digit in that column.
- 19999 is greater than 2000.
How to add and subtract whole numbers
How to add whole numbers
To add whole numbers using the column method:
- Write the numbers in a vertical list, lining up the unit digits.
- Start on the right-hand side, the unit column. Add the digits in the column.
- If the total is less than 10, write the digit in the answer space.
- If the total is 10 or more, write the units digit in the answer space for the column and carry the tens digit to the next column on the left.
- Move left to the next place value column. Add the digits in the column and add any digit that was carried to this column.
- Repeat the addition process in each column until the calculation is complete.
Follow the working out below
How to subtract whole numbers
To subtract whole numbers using the column method:
- Write the larger number above the smaller number in a vertical list, lining up the unit digits.
- Column subtraction works from right to left.
- Start with the unit column on the right-hand side, subtract the bottom digit from the top digit, write the answer in the answer space.
- Move left to the next column.
- Complete the subtraction process for each column until the calculation is complete.
If the top digit is smaller than the bottom digit, regrouping A process where groups of 10 are borrowed from one column and given to another, eg 82 is 8 tens and 2 units, which can be regrouped as 7 tens and 12 units. It is also known as exchanging. the number.
Follow the working out below
GCSE exam-style questions
- Add 912, 56 and 1804.
912 + 56 + 1804 = 2772
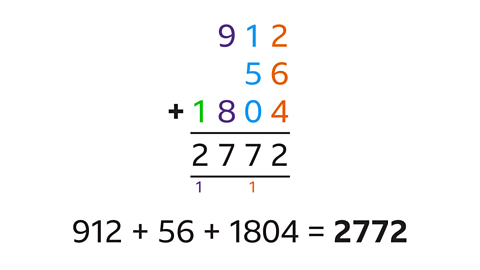
- Write the numbers one under another lining up the units column.
- Starting at the right, add up each column of digits.
- Find the difference between 324 and 109.
324 – 109 = 215
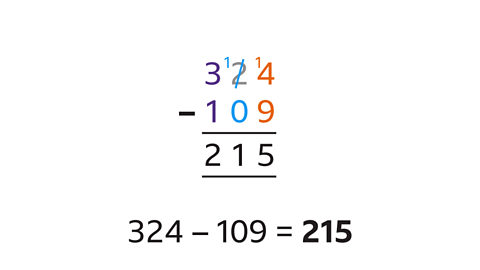
To find the difference between a pair of numbers subtract the smaller number from the larger number.
How to multiply and divide whole numbers
How to multiply whole numbers
Long multiplication may be written using the grid method or the column method.
To multiply whole numbers using the grid method:
- To multiply a 3-digit number by a 2-digit number use a 2 × 3 grid.
- Label the sides of the grid with the place valueThe value of a digit that relates to its position or place in a number, eg in 1482 the digits represent 1 thousand, 4 hundreds, 8 tens and 2 ones. of the digits in the numbers.
- Work out the productThe result of multiplying one number by another, eg the product of 4 and 5 is 20 since 4 × 5 = 20 of the place values for each cell.
- Add the products in the cells to complete the calculation.
To multiply whole numbers using the column method:
- Write the numbers vertically lining up the unit digitOne of the symbols of a number system, most commonly the symbols 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9..
- Multiply the top number by the unit digit of the bottom number working right to left.
- Write the answers in the first row of the working space.
- Write a zero in the unit position on the second row of the working space to show the number has been multiplied by ten.
- Multiply the top number by the tens digit of the bottom number.
- Write the answers in the second row of the working space.
- Add the working answers to complete the calculation.
Different methods of multiplication may be used. Refresh your knowledge of Napier’s method, the area/grid method and short multiplication.
Follow the working out below
How to divide whole numbers
To divide whole numbers using short division (sometimes called the bus stop method):
- Write the question in bus stop form:
- The dividing digitOne of the symbols of a number system, most commonly the symbols 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9. is the divisorThe number by which another is divided, eg in the calculation 30 ÷ 6 , the divisor is 6. and goes outside the bus stop.
- The dividendIn division, the number that is divided, eg in the calculation 30 ÷ 6, 30 is the dividend. goes inside the bus stop.
- The answer quotientThe result of a division, eg in the calculation 30 ÷ 6 = 5, the quotient is 5. will be written on the top of the bus stop.
- Work from left to right dividing each digit in turn.
- If there is a remainder, it becomes the tens digit for the next division.
Follow the working out below
GCSE exam-style questions

- Work out 3584 ÷ 7.
3584 ÷ 7 = 512
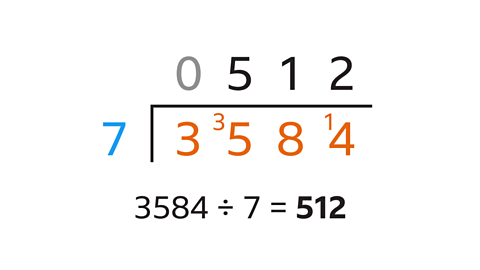
- Draw a ‘bus stop’ with 7 on the left outside and 3584 inside.
- Work from left to right dividing by 7.
- 3 ÷ 7 is 0 remainder 3.
- Write 0 above the 3 and carry the 3 to the next digit (5) to give 35.
- 35 ÷ 7 is 5 remainder 0.
- Write 5 about the 5.
- 8 ÷ 7 is 1 remainder 1.
- Write the 1 above the 8 and carry the 1 to the next digit (4) to give 14.
- 14 ÷ 7 is 2.
- Write 2 above the 4.
The calculation is complete.
- Use the column method to work out the product of:
93 × 52
93 × 52 = 4836

- Write the numbers vertically lining up the unit digits.
- Multiply 93 by 2 to get 186.
- Then multiply 93 by 50:
- First write down a zero in the units column to show that the number is multiplied by ten.
- Then multiply 93 by 5 to get 4650.
- Add the working rows 186 + 4650 = 4836.
- Use the grid method to work out the product of:
18 × 23
18 × 23 = 414
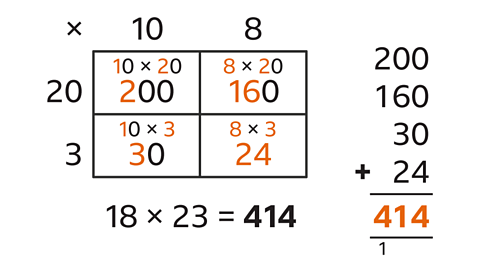
Find the product by multiplying 18 by 23:
- Draw a 2 × 2 grid.
- Label the sides with the place values of each digit.
- 18 is 10 + 8.
- 23 is 20 + 3.
- Write the product of the place values in cells of the grid.
- Add the products to complete the calculation.
Quiz – Whole numbers
Practise what you've learned about whole numbers with this quiz. The questions change each time you try, so keep testing your knowledge.
Now you've revised whole numbers, why not learn about how to round numbers?
More on Number
Find out more by working through a topic
- count2 of 15

- count3 of 15

- count5 of 15
