What are the key learning points?
The concentration of a solution can be calculated from the number of moleA mole of a substance is its relative atomic mass in grams. of a substance and the volume of solutionA mixture made when a solute (usually a solid) dissolves into a solvent (a liquid). Sea water is a solution of salt dissolved into water. it has been dissolved in.
A titration is practical technique where two solutions are accurately reacted with each other. Titrations be used to calculate unknown concentrations of solutions and to identify unknown compounds.
Avogadro’s Law states that equal volumes of any gas will contain the same numbers of particles under the same conditions.
For a chemical process, atom economy is a measure of the amount of atoms in the reactants that end up as useful products. Chemists aim for high atom economies in their reactions.
How to calculate the concentration of a solution (Higher tier only)
The concentrationThe amount of a substance that has been dissolved in a certain amount of solution. Measured in mol/dm3 (moles per decimetre cubed). of a solution depends on the number of moleA mole of a substance is its relative atomic mass in grams. of the soluteThe solid (or occasionally a gas) which dissolves into a solvent (liquid) in order to make a solution. For example, the main solute in sea water is sodium chloride. and the volume of the solution.
You can therefore calculate the concentration of a solutionA mixture made when a solute (usually a solid) dissolves into a solvent (a liquid). Sea water is a solution of salt dissolved into water. in mol/dm3 using the number of moles in the solution and the volume in dm3.
\(concentration~in~mol/dm^3 = \frac{number~of~moles}{volume~in~dm^3}\)
Divide volumes in cm3 by 1000 to convert them into dm3.
Question
0.5 mol of solute is dissolved in 250 cm3 of solution.
Calculate the concentration of the solution.
Answer
250 cm3 = 250 ÷ 1000 = 0.25 dm3
Concentration = 0.5 ÷ 0.25 = 2.0 mol/dm3
How to calculate the number of moles of a solute
The equation above can be rearranged to find the number of moles of solute in a solution.
Rearranging the equation: number of moles = concentration (mol/dm3) × volume (dm3)
Question
Calculate the amount of solute dissolved in 2 dm3 of a 0.1 mol/dm3 solution.
Answer
Amount = 0.1 × 2 = 0.2 mol
How to calculate the volume of a solution
This equation above can also be rearranged to find the volume of a solution.
Rearranging the equation:
volume (dm3) = moles ÷ concentration (dm3)
Question
Calculate the volume of a 2 mol/dm3 solution that contains 0.5 mol of solute.
Answer
Volume = 0.5 ÷ 2 = 0.25 dm3
Note that 0.25 dm3 is the same as 250 cm3 (0.25 × 1000).
How to change the units of concentration
Concentrations can also be expressed in grams per decimetre cubed (g/dm3).
Use the relative formula mass (Mr) to convert the two units of concentration.
Question
The concentration of a solution of sodium hydroxide, NaOH, is 0.5 mol/dm3.
What is this concentration in g/dm3?
Ar of Na = 23, O = 16, H = 1.
Answer
Concentration (g/dm3) = concentration (mol/dm3) × Mr
Mr of NaOH = 23 + 16 + 1 = 40.
Concentration (g/dm3) = 0.5 × 40 = 20 g/dm3.
What are titrations?
A titration is an experimental technique that is used to accurately find the volumes of acidCorrosive substance which has a pH lower than 7. Acidity is caused by a high concentration of hydrogen ions.and alkaliA base which is soluble in water. A base is a substance which neutralises an acid. solutions that will react together.
This information can be used in calculations to work out the concentration of an unknown solution.
How to carry out a titration
The equipment below needs to be prepared before use in a titration:
A pipetteA piece of apparatus used to measure accurate and repeatable volumes of liquid. should be rinsed with deionised water and then with the solution which is it is going to be used to measure.
A safety pipette filler should be used to draw up the solution until the bottom of the meniscusThe curved upper surface of a liquid in a tube. is on the line and the solution is then released into a conical flask.
A buretteA piece of apparatus used to add varying but measured volumes of solution during a titration. is rinsed with deionised water and then with the solution which is going to be used in the burette, ensuring the solution passes through the jet.
The burette is then filled with the solution, ensuring the jet is filled.
The slideshow below shows the steps involved in titrating an acid into an alkali.
The same steps could be used to titrate an alkali into an acid.
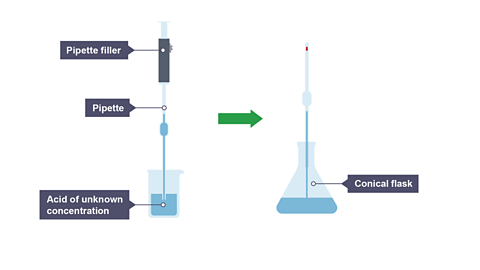
Image caption, 1. A pipette and pipette filler is used to transfer 25 cm³ of an acid of unknown concentration into a conical flask.
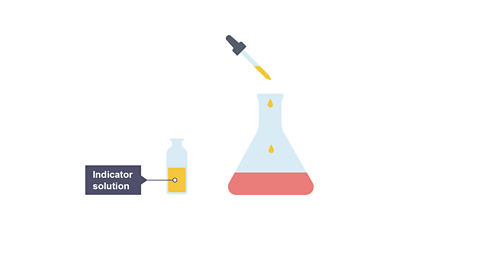
Image caption, 2. A few drops of an indicator solution (e.g. methyl orange) is added to the conical flask.

Image caption, 3. A burette is used to add an alkali of known concentration to the acid. The burette tap is closed as soon as the indicator changes colour – this indicates the neutralisation is complete.
1 of 3
- Use the pipette and pipette filler to add a measured volume of hydrochloric acid solution to a clean conical flask.
- Add a few drops of indicatorA chemical that gives a colour change in acidic, alkaline or neutral solutions. and put the conical flask on a white tile.
- Fill the burette with sodium hydroxide solution and note the initial reading.
- Slowly add the alkali from the burette to the acid in the conical flask, swirling to mix. Add the alkali drop by drop toward the end for maximum accuracy.
- Stop adding the alkali when the indicator first permanently changes colour (the end point). Note the final reading.
- Repeat steps 1 – 5, until you get concordant (agreeing) titres.
Two common indicators used in titrations are methyl orange and phenolphthalein:
| Indicator | Colour in acid | Colour in alkali |
|---|---|---|
| Methyl orange | Red | Yellow |
| Phenolphthalein | Colourless | Pink |
To ensure accuracy in a titration:
- Read volumes from the bottom of the meniscus.
- Add the solution from the burette drop-by-drop near the end point.
- Swirl the conical flask during the titration to ensure the solutions are mixed.
How to record the results of a titration
Record the results in a table.
| Titration | Initial burette reading /cm3 | Final burette reading /cm3 | Titre /cm3 |
|---|---|---|---|
| Rough | 0.0 | 25.8 | 25.8 |
| 1 | 0.0 | 24.6 | 24.6 |
| 2 | 24.6 | 49.3 | 24.7 |
Record your readings to one decimal place.
For example, a reading of 0 cm3 or 24 cm3 on the burette must be recorded as 0.0 cm3 and 24.0 cm3.
The titre is the volume added (the difference between the end and start readings).
A rough titration is carried out to get an idea of the end point of the titration so the accurate titration may be carried out more quickly.
The solution in the burette should be added dropwise, whilst swirling the conical flask, as you approach the end point.
Concordant titres are within 0.2 cm3 of each other.
The results of titrations 1 and 2 are concordant titres.
Question
Calculate the average titre from the figures in the table. Ignore the rough titration.
Answer
average titre = \(\frac{24.6~+~24.7}{2}\) = 24.65cm3
Prescribed practical C8: Titration
Please use the link below to access the article on: Prescribed practical (C8) - Titration
How to use titrations for calculations (Higher tier only)
The results of a titration can be used to calculate the concentration of a solution, the volume of a solution, or to identify an unknown compoundA substance formed when two or more elements are chemically combined..
How to calculate a concentration using titration
Worked example
In a titration, 25.0 cm3 of 0.1 mol/dm3 sodium hydroxide solution are exactly neutralised by 20.0 cm3 of a dilute solution of hydrochloric acid.
Calculate the concentration of the hydrochloric acid solution in mol/dm3.
Step 1: Calculate the number of moles of the solution of known concentration
moles = concentration (mol/dm3) × volume (dm3)
sodium hydroxide solution has a concentration of 0.1 mol/dm3
volume of sodium hydroxide = 25.0 cm3 = 25.0 ÷ 1000 = 0.025 dm3
moles of sodium hydroxide = 0.1 × 0.025 = 0.0025 mol
Step 2: Use the ratio from the equation to find the moles of the solution of unknown concentration
Sodium hydroxide and hydrochloric acid react according to the following equation:
NaOH + HCl → NaCl + H2O
The mole ratio between NaOH : HCl is therefore 1 : 1
Step 3: Calculate the unknown concentration
concentration (mol/dm3) = \(\frac{moles}{volume~(dm^3)}\)
moles of hydrochloric acid = 0.0025 mol (from step 2)
volume of hydrochloric acid = 20.0 cm3 = 20 ÷ 1000 = 0.02 dm3
concentration of hydrochloric acid = \(\frac{0.0025}{0.02}\) = 0.125 mol/dm3
Question
In a titration, 25.0 cm3 of 0.2 mol/dm3 sodium hydroxide solution is exactly neutralised by 22.7 cm3 of a dilute solution of hydrochloric acid.
The equation for the reaction is:
NaOH + HCl → NaCl + H2O
Calculate the concentration of the hydrochloric acid in mol/dm3.
Answer
Step 1: Calculate the moles of the solution of known concentration
moles = concentration (mol/dm3) × volume (dm3)
volume of sodium hydroxide = 25.0 cm3 = 25 ÷ 1000 = 0.025 dm3
moles of sodium hydroxide = 0.2 × 0.025 = 0.005 mol
Step 2: Use the ratio to find moles of the solution of unknown concentration
Use ratio to find moles of the solution of unknown concentration
From the equation the NaOH : HCl ratio is 1 : 1
moles of hydrochloric acid = 0.005 mol
Step 3: Calculate the unknown concentration
Concentration (mol/dm3) = \(\frac{moles}{volume~in~dm^3}\)
volume of hydrochloric acid = 22.7 cm3 = 22.7 ÷ 1000 = 0.0227 dm3
concentration of hydrochloric acid = \(\frac{0.005}{0.0227}\) = 0.220 mol/dm3
How to calculate a volume using titration
In this type of calculation you need to work out the volume of one solution needed to exactly neutralise a certain volume of another solution.
Worked example
25.0 cm3 of 0.3 mol/dm3 sodium hydroxide solution is exactly neutralised by 0.1 mol/dm3 sulfuric acid.
Calculate the volume of sulfuric acid required.
Step 1: Calculate the number of moles of the solution of known concentration and volume
moles = concentration (mol/dm3) × volume (dm3)
The sodium hydroxide solution has a concentration of 0.3 mol/dm3.
volume of sodium hydroxide solution = 25.0 ÷ 1000 = 0.025 dm3
Number of moles of sodium hydroxide = 0.3 × 0.025 = 0.0075 mol
Step 2: Use the ratio from the equation to find the moles of the solution of unknown volume
Sodium hydroxide and sulfuric acid react according to the following equation:
2NaOH + H2SO4 → Na2SO4 + 2H2O
The mole ratio between NaOH : H2SO4 is therefore 2 : 1
moles of sulfuric acid = 0.0075 ÷ 2 = 0.00375 mol
Step 3: Calculate the unknown volume
By rearranging the concentration equation:
volume (dm3) = \(\frac{moles}{concentration~(mol/dm^3)}\)
concentration of sulfuric acid = 0.1 mol/dm3 (from question)
moles of sulfuric acid = 0.00375 mol (from step 2)
volume of sulfuric acid = \(\frac{0.00375}{0.1}\) = 37.5 cm3
How to identify an unknown compound using titration
Two types of unknown compounds can be identified using a titration:
- A compound with an unknown element – e.g. MOH (where M is an unknown metal).
- A hydrated compound with an unknown degree of hydration – e.g. Na2CO3·xH2O (where x is the unknown degree of hydration).
In both cases the compound can be fully identified by calculating its Mr.
Worked example
2.8 g of an unknown metal hydroxide, MOH, was dissolved in water to give 25.0 cm3 of solution.
The solution was reacted with 2 mol/dm3 hydrochloric acid in a titration.
25.0 cm3 of the hydrochloric acid was required for neutralisation.
Identify the unknown metal hydroxide.
Neutralisation equation: MOH + HCl → MCl + H2O
Ar of O = 16, H = 1.
Step 1: Calculate the number of moles of the solution of known concentration and volume
moles = concentration (mol/dm3) × volume (dm3)
The hydrochloric acid has a concentration of 2 mol/dm3.
volume of hydrochloric acid = 25.0 ÷ 1000 = 0.025 dm3
Number of moles of hydrochloric acid = 2 × 0.025 = 0.05 mol
Step 2: Use the ratio from the equation to find the moles of the solution of the unknown compound
According to the equation the mole ratio between MOH : HCl is 1 : 1
moles of MOH in the 25.0 cm3 solution = 0.05 mol
Step 3: Calculate the Mr of the unknown compound
Rearranging the equation moles = \(\frac{mass}{M _r}\) gives Mr = \(\frac{mass}{moles}\)
The mass of MOH in 25.0 cm3 of solution = 2.8 g
The number of moles of MOH in 25.0 cm3 of solution = 0.05 mol
Mr of MOH = \(\frac{2.8}{0.05}\) = 56
Step 4: Subtract from the Mr to identify the unknown metal
Mr of MOH = 56
Ar of O = 16, H = 1
Ar of M = 56 – (16 + 1) = 39
Using the periodic table; M is potassium.
Question
2.86 g of sodium carbonate of unknown hydration, Na2CO3·xH2O, was dissolved in water to give 25.0 cm3 of solution.
The solution was reacted with 1 mol/dm3 hydrochloric acid in a titration.
20.0 cm3 of the hydrochloric acid was required for neutralisation.
Calculate the degree of hydration of the sodium carbonate.
Neutralisation equation: Na2CO3 + 2HCl → 2NaCl + H2O + CO2
Mr of Na2CO3 = 106, H2O = 18.
Step 1: Calculate the number of moles of the solution of known concentration and volume.
moles = concentration (mol/dm3) × volume (dm3)
The hydrochloric acid has a concentration of 1 mol/dm3.
volume of hydrochloric acid = 20.0 ÷ 1000 = 0.02 dm3.
Number of moles of hydrochloric acid = 1 × 0.02 = 0.02 mol.
Step 2: Use the ratio from the equation to find the moles of the solution of the unknown compound.
According to the equation the mole ratio between Na2CO3 : HCl is 1 : 2
moles of Na2CO3·xH2O in the 25.0 cm3 solution = 0.02 ÷ 2 = 0.01 mol
Step 3: Calculate the Mr of the unknown compound.
Mr = \(\frac{mass}{moles}\)
The mass of Na2CO3·xH2O in 25.0 cm3 of solution = 2.86 g
The number of moles of Na2CO3·xH2O in 25.0 cm3 of solution = 0.01 mol
Mr of Na2CO3·xH2O = \(\frac{2.86}{0.01}\) = 286
Step 4: Subtract from the Mr to calculate the degree of hydration.
Mr of Na2CO3·xH2O = 286
Mr of Na2CO3 = 106
Mr of ‘xH2O’ = 286 – 106 = 180
Mr of H2O = 18
x = \(\frac{180}{18}\) = 10
and the formula of the hydrated compound is Na2CO3·10H2O
What is Avogadro's law? (Higher tier only)
Avogadro's law states:
- equal volumes of different gases contain an equal number of particles under the same conditions of temperature and pressure.
This means that equal numbers of moles of gases occupy the same volume under the same conditions of temperature and pressure.
For example:
1 mol of hydrogen gas occupies the same volume as 1 mol of methane gas.
10 mol of nitrogen monoxide gas occupy the same volume as 10 mol of argon gas.
Key fact
The volume of 1 mol of any gas at room temperature and pressure is 24 dm3/24000 cm3.
Equal numbers of moles of any gas occupy the same volume.
How to make gas volume calculations
You can convert between the volume of a gas and the number of moles of a gas using the following equations:
gas volume (dm3) = number of moles × 24
number of moles = \(concentration~in~mol/dm^3 = \frac{gas~volume~in~dm^3}{24}\)
Note: if the volume of gas is in cm3, use 24000 rather than 24.
Example
Calculate the volume (in cm3) occupied by 4.4 g of CO2(g) at room temperature and pressure.
Mr of CO2 = 44
Answer
Number of moles of CO2 = \(\frac{mass}{M_r}\) = \(\frac{4.4}{44}\) = 0.1 mol
gas volume (cm3) = moles × 24000 = 0.1 × 24000 = 2400 cm3.
Question
Calculate the volume of hydrogen gas produced in dm3 when 0.3 g of magnesium ribbon react with excess hydrochloric acid.
Mg(s) + 2HCl(aq) → MgCl2(aq) + H2(g)
Ar of Mg = 24
Answer
moles of Mg = \(\frac{0.3}{24}\) = 0.0125 mol
moles of H2 = 0.0125 mol (as 1:1 ratio of Mg : H2)
volume of H2 = moles × 24 = 0.0125 × 24 = 0.3 dm3
How to use Avogadro's law?
In reactions where all of the reactantThe chemical present at the start of a reaction. Reactants appear on the left of a chemical equation, before the arrow →. and productA chemical which is made in a chemical reaction. Products are written on the right of a chemical equation, after the arrow (→). are gases, the mole ratio can be used to calculate the volumes of gases.
For example:
Hydrogen reacts with chlorine to form hydrogen chloride:
H2(g) + Cl2(g) → 2HCl(g)
The mole ratio of H2 : Cl2 : HCl is 1 : 1 : 2.
Therefore:
1 cm3 of hydrogen gas would react with 1 cm3 of chlorine gas to produce 2 cm3 of hydrogen chloride gas.
20 dm3 of hydrogen would react with 20 dm3 of chlorine gas to produce 40 dm3 of hydrogen chloride gas.
Question
Nitrogen reacts with hydrogen to produce ammonia:
N2(g) + 3H2(g) → 2NH3(g)
Calculate the volume of ammonia that can be produced from 150 cm3 of hydrogen and an excess of nitrogen.
Answer
The mole ratio of hydrogen to ammonia is 3:2
Volume of ammonia = \(\frac{150}{3}\)× 2 = 100 cm3.
What is atom economy?
Some products in chemical reactions are desired, and others are not desired (sometimes called by-productA product from a side reaction which is formed during the creation of another product, usually an undesirable product.).
For example, in the manufacture of hydrogen from methane and steam:
methane + steam → hydrogen + carbon monoxide
The hydrogen is the desired product and the carbon monoxide is the by-product (not-desired).
In a chemical reaction atoms in the reactants rearrange themselves to form the products.
Atom economy is a measure of the amount of the reactant atoms that end up as useful products.
How to calculate percentage atom economy
The percentage atom economy of a reaction is calculated using this equation:
atom economy = \(\frac{mass~of~desired~product}{total~mass~of~products}\) x 100
Note: Mr values can be used for mass in atom economy calculations.
The highest possible value of atom economy is 100%, when all the reactant atoms end up in the desired product.
If the atom economy is 50%, for example, then half the reactant atoms end up in the desired product or products.
It is important to aim for a high atom economy in chemical processes for two reasons:
Sustainability: High atom economy reactions help to preserve natural resources of chemicals.
Economic: It is less expensive to have a process with a high atom economy as the majority of the atoms in the reactants end up in useful products.
Example
Hydrogen can be manufactured by reacting methane with steam:
CH4(g) + H2O(g) → 3H2(g) + CO(g)
Calculate the atom economy for the reaction. (Ar of H = 1, Ar of C = 12, Ar of O = 16)
Answer
H2 is the desired product, CO is the by-product.
Mr of H2 = 2 × 1 = 2
Mass of desired product = 3 × 2 = 6 (there are three H2 in the balanced equation)
Mr of CO = 12 + 16 = 28
Total Mr of all products = 3 × 2 + 28 = 34
Atom economy = \(\frac{mass~of~desired~product}{total~mass~of~products}\) = 100
Atom economy = \(\frac{6}{34}\) x 100
Atom economy = 17.6%
Question
Ethanol (C2H5OH) can be produced by the fermentation of glucose (C6H12O6), producing carbon dioxide as a by-product.
Calculate the percentage atom economy for this process.
C6H12O6 → 2C2H5OH + 2CO2
Ar of C = 12, H = 1, O = 16
Answer
C2H5OH is the desired product: Mr = (2 × 12) + (5 × 1) + 16 + 1 = 46
Mass of desired product = 2 × 46 = 92
CO2 is the undesired product: Mr = 12 + (2 ×16) = 44
Total mass of products = (2 × 46) + (2 × 44) = 180
Atom economy = \(\frac{mass~of~desired~product}{total~mass~of~products}\) = 100
Atom economy = \(\frac{92}{180}\) x 100
Atom economy = 51.1%
How much do you know about quantitative chemistry 2?
More on Unit 2: Further chemical reactions, rates and equilibrium, calculations and organic chemistry
Find out more by working through a topic
- count7 of 9

- count8 of 9
- count9 of 9

- count1 of 9
