Key points about multiples and factors
An Integers are numbers with no fraction or decimal part. They can be positive, negative or zero. 42, –8, and 10,000 are examples of integers. is both a factor and a An integer that is in the multiplication table of a specific number. For example, 20 is a multiple of ten because 20 is in the ten times table. of itself.
A A whole number greater than 1 that has exactly two factors, itself and 1, eg 2 is a prime number, its factors are 2 and 1. has two factors, itself and one.
A A square number is the result of multiplying a whole number by itself, eg 9 is a square number because 3×3 = 9. always has an odd number of factors.
Refresh your knowledge with these guides on factors and multiples and product of prime factors.
Check your understanding
What are multiples and factors?
To work out the 5th multiple of a number, for example, multiply the number by 5.
To list all the A number or variable that divides exactly into a term. of a number, find all the Two numbers that have a product of a selected whole number, eg, 3 and 4 have a product of 12, so 3 and 4 are a factor pair of 12. A whole number may have one or more factor pairs. :
The first factor pair is always 1 and the number itself.
Consider whether the number is divisible, in turn, by 2, 3, 4, etc.
- Divide to find the other factor of the pair.
All the factors are found when the next value is part of a pair that has already been identified.
Follow the working out below
GCSE exam-style questions
- Find the difference between the 3rd multiple of 7 and the 4th multiple of 6.
The difference is 3.
The 3rd multiple of seven is 7 × 3 = 21.
The 4th multiple of six is 6 × 4 = 24.
The difference is 24 – 21 = 3.
- List the factor pairs of 12.
The factor pairs of 12 are 1 and 12, 2 and 6, 3 and 4.
The first factor pair is 1 and the number itself (12).
12 is divisible by 2, 12 ÷ 2 = 6, the second factor pair is 2 and 6.
12 is divisible by 3, 12 ÷ 3 = 4, the third factor pair is 3 and 4.
12 is divisible by 4, 12 ÷ 4 = 3, This pair (4 and 3) has already been established/found.
All the factor pairs have been found.
The factor pairs of 12 are 1 and 12, 2 and 6, 3 and 4.
What are prime, square and cube numbers?
To confirm that a number is A whole number greater than 1 that has exactly two factors, itself and 1, eg 2 is a prime number, its factors are 2 and 1. :
Check that the number has exactly two A number or variable that divides exactly into a term., the number itself and 1.
Numbers that have more than two factors are called A number with more than two factors. Composite numbers are not prime numbers. 20 is a composite number and has six factors (1, 2, 4, 5, 10, 20). .
1 has one factor and can be referred to as a unit. 1 is not a prime number.
To confirm that a number is a A square number is the result of multiplying a whole number by itself, eg 9 is a square number because 3×3 = 9.:
Check that the number can be expressed as the The result of multiplying one number by another, eg the product of 4 and 5 is 20 since 4 × 5 = 20 of two equal Integers are numbers with no fraction or decimal part. They can be positive, negative or zero. 42, –8, and 10,000 are examples of integers. (an integer multiplied by itself). This can be written using The notation in which a product such as 𝑛 × 𝑛 × 𝑛 × 𝑛 is recorded as 𝑛⁴. In this example the number 4 is called the index (plural indices) and the number represented by 𝑛 is the base. : 3² is 3 squared.
A square number cannot be a prime number.
A square number has an odd number of factors.
To confirm that a number is a A cube number is the result of a number being multiplied by itself and then by itself again, eg 8 is a cube number because 2 × 2 × 2 = 8.:
- Check that the number can be expressed as the product of three equal integers. A cube may be written using index notation: 5³ is 5 cubed.
Follow the working out below
GCSE exam-style questions
- Which number is both a square number and a cube number?
8 16 32 64
64 is both a perfect square (64 = 8 × 8) and a cube.
(64 = 4 × 4 × 4).
- 8 has four factors, 8, 4, 2 and 1.
It is a composite number and also a cube number:
8 = 2 × 2 × 2.
- 16 has five factors, 16, 8, 4, 2 and 1.
It is a composite number and a perfect square: 16 = 4 × 4.
- 32 has six factors, 32, 16, 8, 4, 2, and 1.
It is a composite number. It is neither a square number nor a cube.
- 64 has seven factors, 64, 32, 16, 8, 4, 2, and 1.
It is a composite number, a square number (64 = 8 × 8) and a cube number
(64 = 4 × 4 × 4).
- Find two prime numbers that add up to 16.
3 + 13 and 5 + 11
Pairs of numbers adding to 16 must be both even or both odd.
2 is the only even prime. 2 + 14 = 16. 14 has more than two factors (1, 2, 7, 14).
Other pairs of even numbers adding to 16 can be ignored (4 + 12, 6 + 10 and 8 + 8), none are prime.
16 = 1 + 15. Neither 1 nor 15 are prime. 1 has one factor. 15 has more than two factors, (1, 3, 5, 15).
16 = 3 + 13. Both 3 and 13 are prime. 3 has two factors, 1 and 3. 13 has two factors 1 and 13.
16 = 5 + 11. Both 5 and 11 are prime. 5 has two factors, 1 and 5. 11 has two factors 1 and 11.
16 = 7 + 9. 7 is prime (two factors, 1 and 7), 9 is not prime (more than two factors, 1, 3 and 9).
3 + 13 = 16 and 5 + 11 = 16.
What is the product of prime factors?
To write a number as a product of its :
- Draw a .
Write the number and draw two branches to give a factor pair, both greater than 1.
Write a factor at the end of each branch and decide if the factor is a prime number.
If yes: The branch does not go any further and the factor is circled to show this.
If no: Split into a further pair of factors, greater than 1.
- Continue this process until the branches all end in A whole number greater than 1 that has exactly two factors, itself and 1, eg 2 is a prime number, its factors are 2 and 1. . These are the prime factors of the number.
- Write the number equal to the factors multiplied together in numerical order.
- Use The notation in which a product such as 𝑛 × 𝑛 × 𝑛 × 𝑛 is recorded as 𝑛⁴. In this example the number 4 is called the index (plural indices) and the number represented by 𝑛 is the base. when a number occurs more than once.
The factor tree of a number can appear different, but the numbers at the end of the branches and the product of prime factors will always be the same.
Follow the working out below
GCSE exam-style questions
- Write 200 as a product of prime factors.
200 = 2³ × 5²
First draw the factor tree for 200.
Start with 200 and draw two branches to give a factor pair. 20 and 10 are used here.
Next find factor pairs for each of 20 and 10.
20 is 2 × 10 and 10 is 2 × 5.
10 can be split into the factor pair 2 and 5.
All the numbers at the end of the branches are prime factors. These are circled.
200 can be written as a product of these prime factors: 200 = 2 × 2 × 2 × 5 × 5.
This can also be written using index notation:
200 = 2³ × 5².
- A number has been written as a product of its prime factors: 2⁷ × 3²
What is the number?
2⁷ × 3² = 1152
2⁷ × 3² =
2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 = 1152
Quiz - Multiples and factors
Practise what you've learned about multiples and factors with this quiz. The questions change each time you try, so keep testing your knowledge.
Higher - Powers and roots
To estimate a A number used multiple times in a multiplication, eg 3² is 3 to the power of 2, 3 squared or 3 × 3. :
Find the powers of above and below the given value.
The power will be between these values.
To estimate the A value whose square is equal to a given number, eg one square root of 25 is 5 since 5² = 25. The square root of 25 is recorded as √25 = 5. However, as well as a positive square root, 25 has a negative square root, since (− 5)² = 25. of a number:
Find the nearest A square number is the result of multiplying a whole number by itself, eg 9 is a square number because 3×3 = 9. above and below the number.
The square root of the number will be between the square roots of the perfect squares.
The estimation may be written as:
An inequality.
An estimated value based on which limit the value is closer to.
Follow the working out below
GCSE exam-style questions
- Between which two consecutive integers does the cube root of 100 lie?
Give the answer as an inequality.
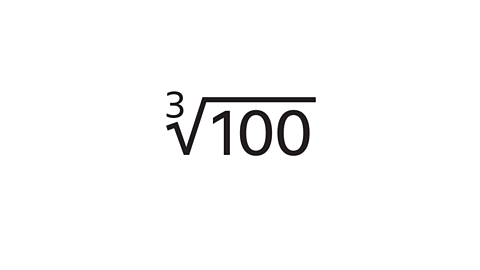
The answer is 4 < \(^{3}\sqrt{100}\) < 5
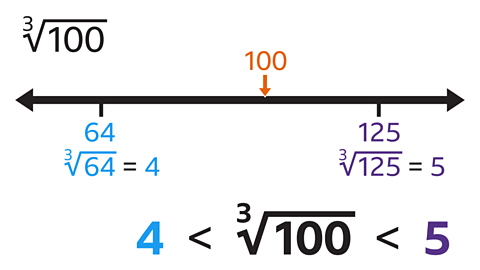
The cube numbers below and above 100 are 64 and 125.
4³ = 64
5³ = 125
The cube root of 100 lies between 4 and 5.
- Which of the four values below is the best estimate for 8·7²?
75 is the best estimate for 8·7².
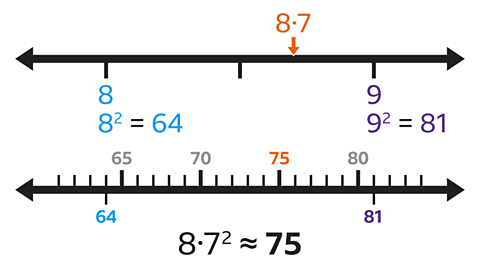
8·7 lies between 8 and 9 and is closer to 9.
8² = 64
9² = 81
8·7² is nearer to 81 than to 64, so 65 and 70 can be discarded.
80 is very close to 81.
Therefore the best estimate for 8·7² is 75.
Higher - Calculating square and cube roots using the product of primes
To work out a root using the product of of a number:
Write the prime factor product without The notation in which a product such as 𝑛 × 𝑛 × 𝑛 × 𝑛 is recorded as 𝑛⁴. In this example the number 4 is called the index (plural indices) and the number represented by 𝑛 is the base. .
Split the The factors of 12 are 1, 2, 3, 4, 6 and 12. The prime factors of 12 are 2 and 3. 12 may be expressed as a product of its prime factors: 12 = 2 × 2 × 3. into:
Two identical groups of A whole number greater than 1 that has exactly two factors, itself and 1, eg 2 is a prime number, its factors are 2 and 1. for a A value whose square is equal to a given number, eg one square root of 25 is 5 since 5² = 25. The square root of 25 is recorded as √25 = 5. However, as well as a positive square root, 25 has a negative square root, since (− 5)² = 25. .
Three identical groups of primes for a .
- Find the product of one group to evaluate the root.
Follow the working out below
GCSE exam-style questions
- As a product of primes, 5184 is 2⁶ × 3⁴.
Find the square root of 5184.
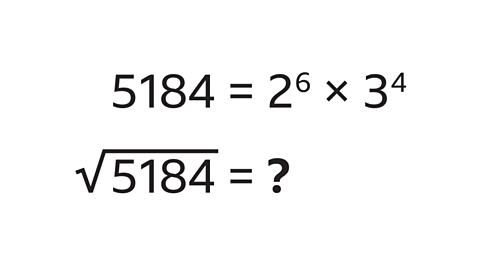
\(^\sqrt{5184}\) = 72
- Write the prime factor product without index notation:
5184 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3 × 3
Split the product of primes into two identical groups of primes for the square root.
Each identical group of primes is 2 × 2 × 2 × 3 × 3 = 72.
- As a product of primes, 250,047 is 3⁶ × 7³.
Find the cube root of 250,047.
The cube root of 250,047 is 63.
- Write the prime factor product without index notation:
250,047 = 3 × 3 × 3 × 3 × 3 × 3 × 7 × 7 × 7.
Split the product of primes into three identical groups of primes for the cube root.
Each identical group of primes is 3 × 3 × 7 = 63.
Higher - Quiz - Multiples and factors
Practise what you've learned about multiples and factors with this Higher quiz. The questions change each time you try, so keep testing your knowledge.
Now you've revised multiples and factors, why not look at order of operations and using negative numbers?
More on Number
Find out more by working through a topic
- count12 of 15
- count13 of 15
- count14 of 15
