Key points about geometric and special sequences
- A linear (or arithmetic) sequence increases or decreases by the same number each time, whereas non-linear sequences have different patterns between the numbers.
- A geometric sequence has a A rule for a sequence that explains how to get from one term to the next. of multiplying by a specific number each time.
- Other types of special non-linear sequences include A sequence where the first difference between numbers is not equal, but the second difference between numbers is equal. and A sequence where each term is found by adding the previous two terms., as well as Triangular numbers can be represented as dots that make a triangular shape. A new row of dots is added each time. The first five triangular numbers are 1, 3, 6, 10, 15., A square number is the result of multiplying a whole number by itself, eg 9 is a square number because 3 x 3 = 9. and A cube number is the result of a number being multiplied by itself and then by itself again, eg 8 is a cube number because 2 x 2 x 2 = 8. numbers. A sequence can also take the form of a picture pattern.
You will need to be confident with arithmetic sequences and the 𝑛th term rule to understand these other types of sequences.
Check your understanding
What are geometric sequences?
- A geometric sequence contains numbers that are multiplied by a certain number each time.
- The number that each term is multiplied by is called the common ratio.
Follow the working out below
GCSE exam-style questions
- What is the missing term in the geometric sequence:
2, 8, __, 128?
32
The terms of a geometric sequence are multiplied by the same number (common ratio) each time.
- Find the common ratio by dividing any term by the previous term, eg 8 ÷ 2 = 4.
- The term-to-term rule is ×4.
- The missing term is 8 × 4 = 32.
Check the answer by finding the 4th term. 32 × 4 = 128, which is correct.
- A geometric sequence starts with 2 and has a common ratio of 5. Another geometric sequence starts with 800 and has a common ratio of 0·25.
What number is in both sequences?
50 is in both sequences.
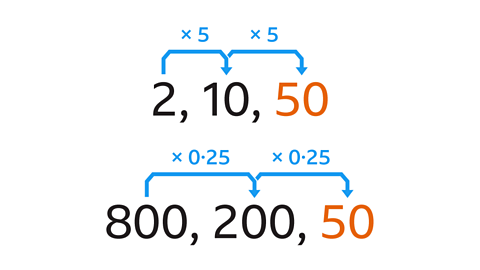
- The terms of the first sequence are multiplied by 5 each time.
- Starting with 2 gives 2, 10, 50, …
- The terms of the second sequence are multiplied by 0.25 each time. This is the same as dividing by 4.
- Starting with 800 gives 800, 200, 50, …
Other special sequences
There are other types of non-linear sequence.
- The sequence of A square number is the result of multiplying a whole number by itself, eg 9 is a square number because 3 x 3 = 9. is found by squaring whole numbers in order from 1.
- The sequence of A cube number is the result of a number being multiplied by itself and then by itself again, eg 8 is a cube number because 2 x 2 x 2 = 8. is found by cubing whole numbers in order from 1.
- The terms of a A sequence where the first difference between numbers is not equal, but the second difference between numbers is equal. do not have the same difference between them, but there is a pattern to the differences. By finding the In a sequence, the second difference is the difference between the first differences., the next term can be found.
- The sequence of Triangular numbers can be represented as dots that make a triangular shape. A new row of dots is added each time. The first five triangular numbers are 1, 3, 6, 10, 15. numbers can be shown by drawing dots that form triangles. A row of dots is added each time.
- The terms of a A sequence where each term is found by adding the previous two terms.-type sequence are created by adding the previous two terms together.
Follow the working out below
GCSE exam-style questions
- What is the next number in the sequence 4, 9, 15, 22,…?
The next number is 30.
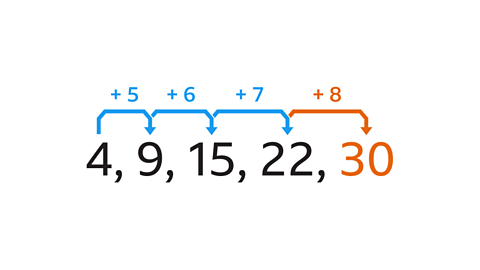
The differences are not the same each time.
The differences increase by 1 each time.
The next difference will be 8.
22 + 8 = 30
- What is the 4th cube number?
64
- A cube number is a number multiplied by itself and then by itself again.
- The 1st cube number is 1 × 1 × 1 = 1³ = 1.
- The 4th cube number is 4 × 4 × 4 = 4³ = 64.
- The first three terms of a Fibonacci-type sequence are 𝑥, 𝑥 + 7 and 2𝑥 + 7. Work out an expression for the 4th term.
3𝑥 + 14
- The terms of a Fibonacci-type sequence are the previous two terms added together.
- For example, the 3rd term is 𝑥 + 𝑥 + 7 = 2𝑥 + 7.
- To find the 4th term, add the 2nd term (𝑥 + 7) and the 3rd term (2𝑥 + 7).
- 𝑥 + 7 + 2𝑥 + 7 = 3𝑥 + 14
Sequences in diagrams
- Sequences can take the form of picture patterns.
- The next pattern can be found by considering how the picture is changing each time.
- Parts of the pattern can be turned into a sequence of number A value in a sequence. The 3rd term is the 3rd value in the sequence, eg 7 is the 3rd term of the sequence 3, 5, 7, 9..
- The A position-to-term rule for sequences. The position number can be substituted into the rule in place of 𝑛 to find the value of that term. of the number sequence can be found and linked to a rule for the 𝑛th pattern.
Follow the working out below
GCSE exam-style questions
- The diagram shows the first four patterns in a sequence. Draw the 5th pattern.
Two sticks are added each time to form another triangle. The 5th pattern has 5 triangles made from 11 sticks.
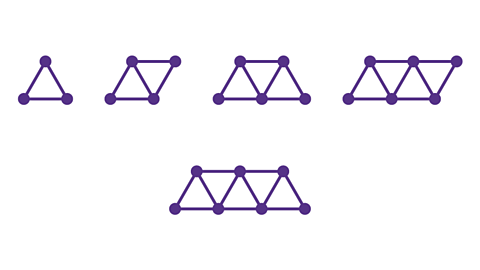
- Find a rule for the number of sticks used in the 𝑛th pattern.
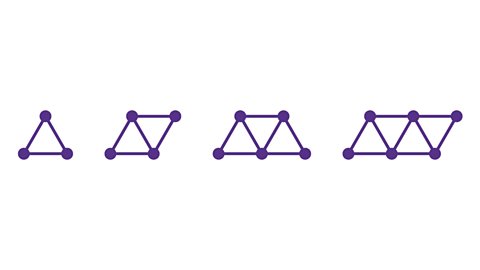
The 𝑛th pattern has 2𝑛 + 1 sticks.
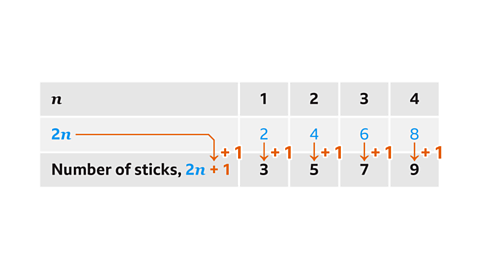
- Write the number of sticks from each pattern to form the number sequence 3, 5, 7, 9.
- Write the pattern number 𝑛 (1, 2, 3 ,4) above the sequence.
- The terms of the sequence are increasing by 2 each time so write the 2 times table in the next row. This is 2𝑛.
- The sequence is always 1 more than the 2 times table, so the rule for the 𝑛th pattern is 2𝑛 + 1.
- The rule for the number of sticks in the 𝑛th pattern is 2𝑛 + 1. What number pattern uses 85 sticks?
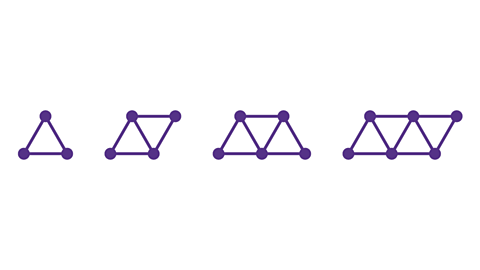
The 42nd pattern.
Find the value for 𝑛 so that the rule equals 85.
Create the equation 2𝑛 + 1 = 85. Solve to give 𝑛 = 42.
The 42nd pattern uses 85 sticks.
Sequences using diagrams – interactive activity
This interactive activity will help you to learn how to work out the 𝑛th term of a linear sequence by creating a series of diagrams.
Quiz – Geometric and special sequences
Practise what you've learned about geometric and special sequences with this quiz.
Now that you have revised geometric and special sequences, why not look at how to factorise expressions?
More on Algebra
Find out more by working through a topic
- count12 of 14
- count14 of 14
